Why a performance boost?
There are several possible reasons for the increase in predictive performance with parcellation resolution. First we note that by ‘applying’ parcellations within the context of the analyses above, we are simply taking the mean value across a contiguous region of vertices. That means that when the region of interest is centered on a single homogenous area that the mean value of the region will have added noise resulting from its heterogeneity. Therefore by increasing the resolution of the parcellation, with a larger number of smaller parcels, each parcel will be less likely to span across multiple distinct structures (i.e., “true regions”). That said, once the resolution becomes too fine grained, subdividing true regions of interest can also introduce noisy estimates.
Consider the figure below which shows a highly simplified example where we assume there are two ground truth ‘real’ regions, R1 and R2, represented by solid line boxes on the top half of the figure. We also consider an individualized parcellation variant on the bottom figure where there are still two ground truth regions R1 and R2, but these regions vary slightly between two subjects, S1 and S2. The columns in this figure consider splitting 4 different sets of parcellations, where each parcel is represented by a dotted box and a shade of gray. The first parcellation (column 1), shows a parcellation with just one parcel. The next two cases, (columns 2 and 3), show two cases for parcellations with two parcels, and the last case, (column 4), shows a parcellation with three equally sized parcels.
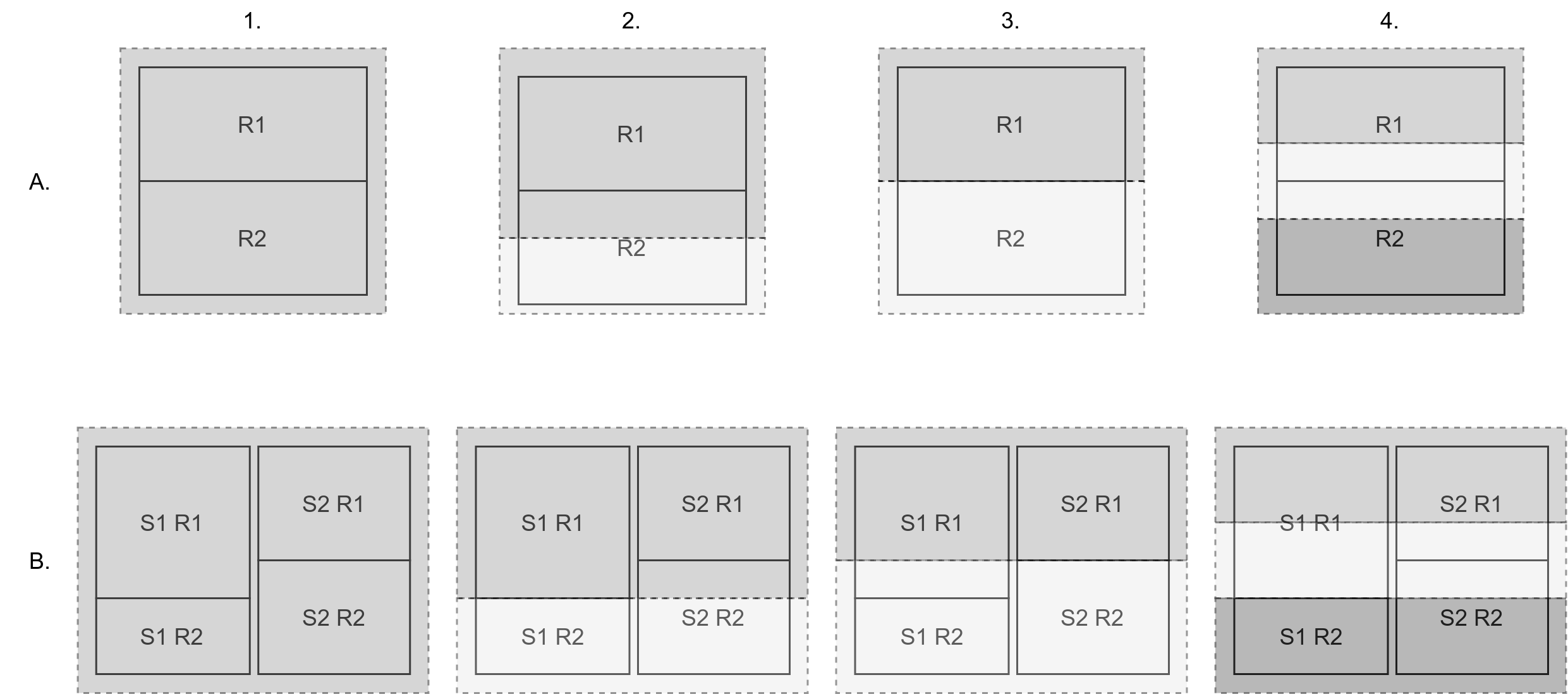
To help provide some intuition around why increasing spatial parcellations resolution improves downstream performance, we consider the simplified example above. Column 1 in both cases represents the case of too coarse spatial resolution, where two meaningful areas with separate information R1 and R2 get averaged together. Columns 2 and 3 are interesting in that they represent the case where the number of parcellations match the baseline ground truth number of regions. In this case we see in A3 that we are able to extract the maximum usable information in the case that the parcellations are exact, but see in A2 that if they are not exact then the parcel with R1 and half of R2 will contain partially corrupted information.
On the other hand, if we consider the individualized parcellation ground truth, then we see that there is no way to match the ground truth with just two parcels, and that both cases like in A2 only allow capturing all usable information from one of the two ground truth regions. Lastly, in column 4, we see that by adding an additional parcellation where are able to in both cases (rows A and B) capture R1 and R2 without information from the other ‘leaking’ in. This is possible because a third parcellation is able to capture the overlap which can then be either ignored by the classifier or potentially exploited in the case that the overlap is meaningful. We additionally make the assumption here that parcels, for example the bottom parcellation in A4, can arrive at the correct mean value for the region without covering the full region. Notably if we were to continue the thought experiment further, considering parcellations of 4, 5, 6, ect… parcels, then this assumption very well might not hold, as it is likely not the case that every vertex in each ground truth region has the exact same value.
What does it mean?
The very existence of a tightly knit scaling between parcellation granularity and out-of-sample phenotypic predictive performance may itself be meaningful, regardless of the exact scaling or range of scaling. Because existing parcellations have a relatively small number of parcels, this scaling suggests that commonly employed parcellations may be too coarse to capture some important inter-individual phenotypic variance. In other words, up to a certain resolution there is still valuable information being washed out from averaging. This increasing marginal utility of smaller and smaller brain regions is fully compatible with the view of the brain as a “hierarchically organized system”, where meaningful cortical areas can be composed at multiple resolutions (Eickhoff 2018). In this sense, as the number of parcels increases it may provide a better mapping onto different resolutions of “true” cortical areas. For example a small number of parcels may only be capturing differences at the highest hierarchical level, but as more parcels are added the gains in performance we found may represent a mapping onto the next meaningful hierarchical resolution of cortical areas.