Extra Results by Parcellation Type

As an alternative modelling choice to the results explored in base results we could instead of using formula log10(Mean_Rank) ~ log10(Size) + C(Parcellation_Type), instead use either log10(Median_Rank) ~ log10(Size) + C(Parcellation_Type), log10(Max_Rank) ~ log10(Size) + C(Parcellation_Type) or log10(Min_Rank) ~ log10(Size) + C(Parcellation_Type). The key variable changing here being the use of median, max or min to summarize ranks, instead of mean rank. Importantly, in this case, the mean or average is still used to summarize across Pipelines, and as in the base comparison we still estimate the region where a powerlaw holds and only model the results within this range, but with the alternate formulation of averaged rank.

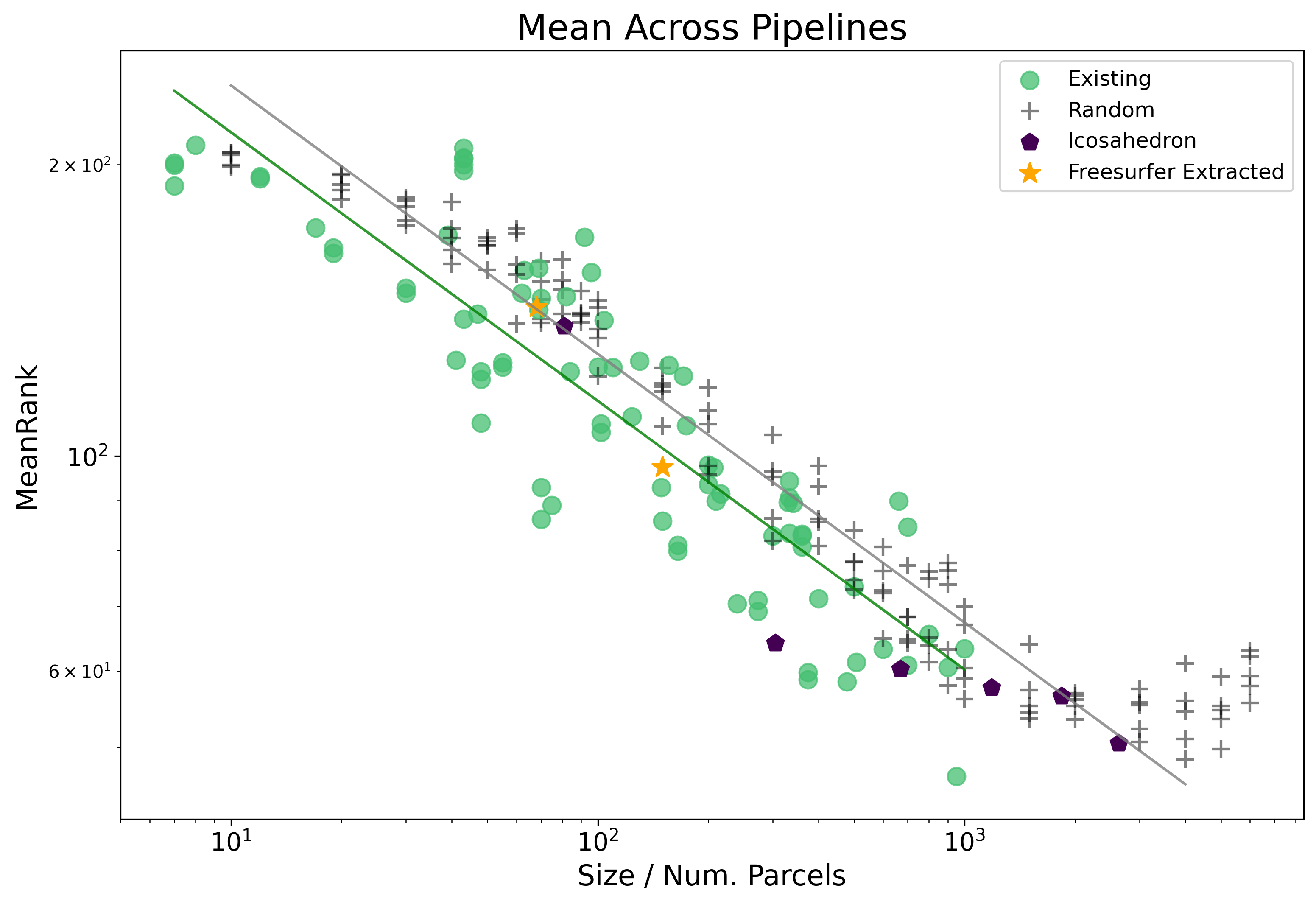
Mean Rank

For ease of comparison we again provide the results from the Mean Rankings here.

OLS Regression Results
Dep. Variable: Mean_Rank R-squared: 0.901
Model: OLS Adj. R-squared: 0.899
Method: Least Squares F-statistic: 459.6
Date: Tue, 11 Jan 2022 Prob (F-statistic): 6.68e-100

coef std err t P>|t| [0.025 0.975]
Intercept 2.6119 0.015 171.406 0.000 2.582 2.642
C(Parcellation_Type)[T.Freesurfer Extracted] 0.0154 0.042 0.367 0.714 -0.067 0.098
C(Parcellation_Type)[T.Icosahedron] -0.0040 0.025 -0.159 0.874 -0.054 0.046
C(Parcellation_Type)[T.Random] 0.0485 0.009 5.597 0.000 0.031 0.066
Size -0.2774 0.007 -41.980 0.000 -0.290 -0.264

fits

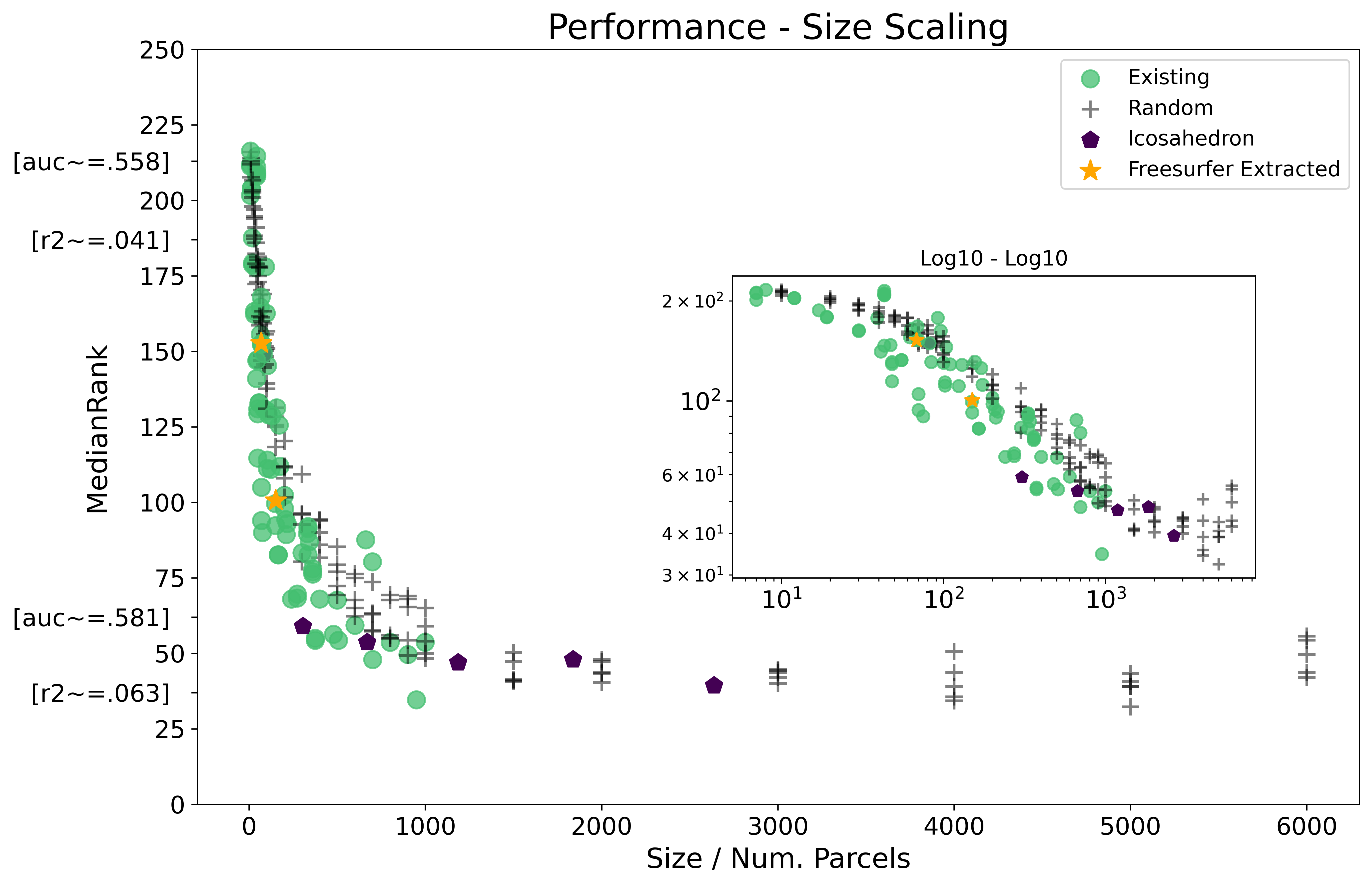
Median Rank

OLS Regression Results
Dep. Variable: Median_Rank R-squared: 0.917
Model: OLS Adj. R-squared: 0.916
Method: Least Squares F-statistic: 561.6
Date: Tue, 11 Jan 2022 Prob (F-statistic): 3.42e-108

coef std err t P>|t| [0.025 0.975]
Intercept 2.7548 0.017 159.032 0.000 2.721 2.789
C(Parcellation_Type)[T.Freesurfer Extracted] 0.0244 0.047 0.515 0.607 -0.069 0.118
C(Parcellation_Type)[T.Icosahedron] -0.0160 0.029 -0.562 0.575 -0.072 0.040
C(Parcellation_Type)[T.Random] 0.0487 0.010 4.947 0.000 0.029 0.068
Size -0.3422 0.007 -46.304 0.000 -0.357 -0.328

As with mean rank, we have only the significant coef. between existing and random parcellations - we plot below just these two lines of fit, as estimated by the OLS, and colored by parcellation type.

fits

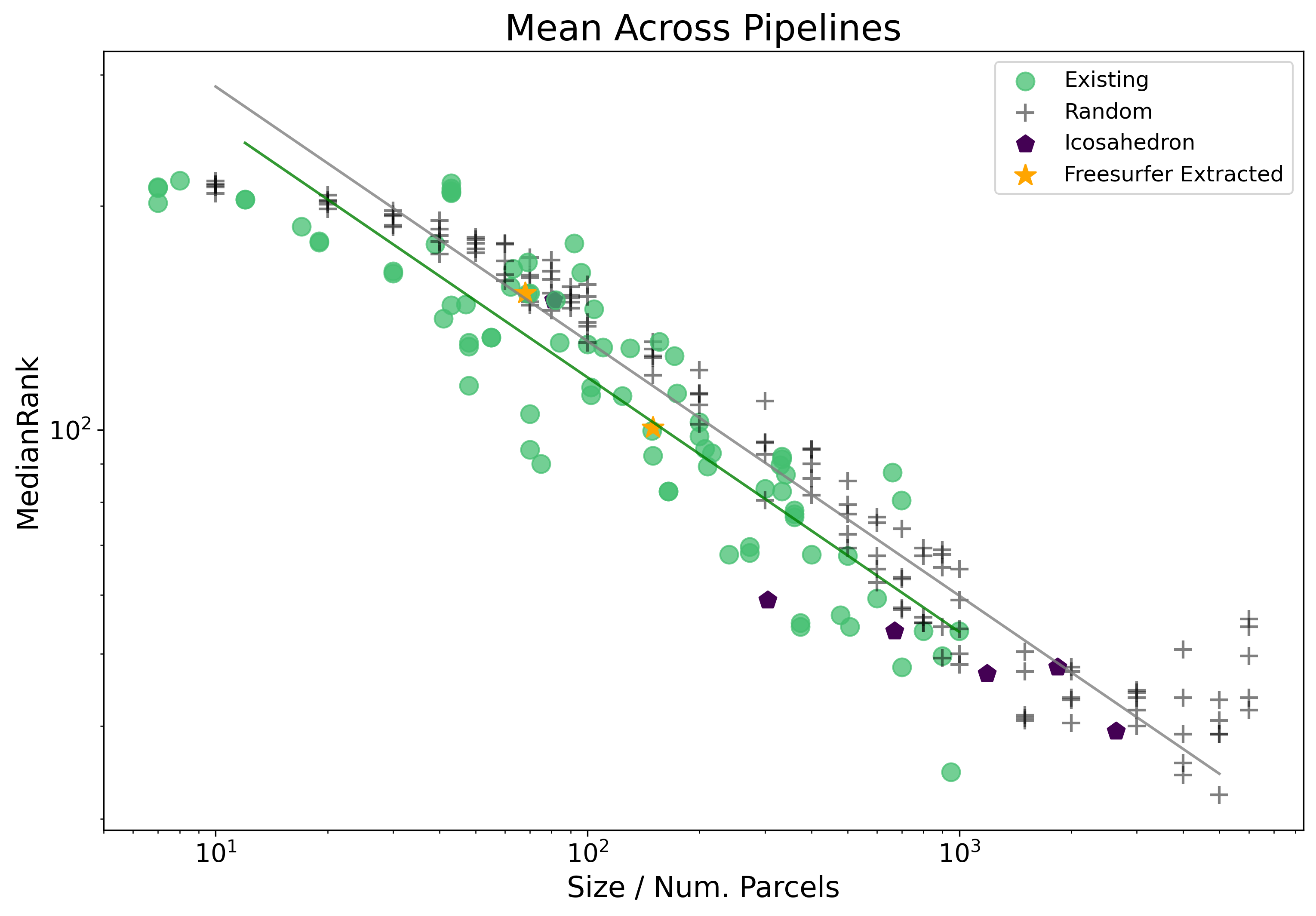
As might be expected, the difference between mean and median ranks ends up being pretty small. Interesting, we actually end up with a more robust power-law scaling fit when using median, as well as a larger size range in which the relationship holds.

A recreation of the main figure from the index page, but with median rank is provided here:

base

Max Rank

Using Max Rank is actually quite different than using mean or median. Instead, what max ranks tells us is essentially the worst case performance of a parcellation across target variables,

OLS Regression Results
Dep. Variable: Max_Rank R-squared: 0.598
Model: OLS Adj. R-squared: 0.589
Method: Least Squares F-statistic: 68.07
Date: Tue, 11 Jan 2022 Prob (F-statistic): 3.38e-35

coef std err t P>|t| [0.025 0.975]
Intercept 2.4070 0.008 287.023 0.000 2.390 2.424
C(Parcellation_Type)[T.Freesurfer Extracted] 0.0394 0.019 2.098 0.037 0.002 0.076
C(Parcellation_Type)[T.Icosahedron] 0.0136 0.011 1.201 0.231 -0.009 0.036
C(Parcellation_Type)[T.Random] 0.0132 0.004 3.287 0.001 0.005 0.021
Size -0.0577 0.004 -16.094 0.000 -0.065 -0.051

To match the plot above, and to limit the complexity of the plot, we just show fits for existing and random type parcellations.

fits

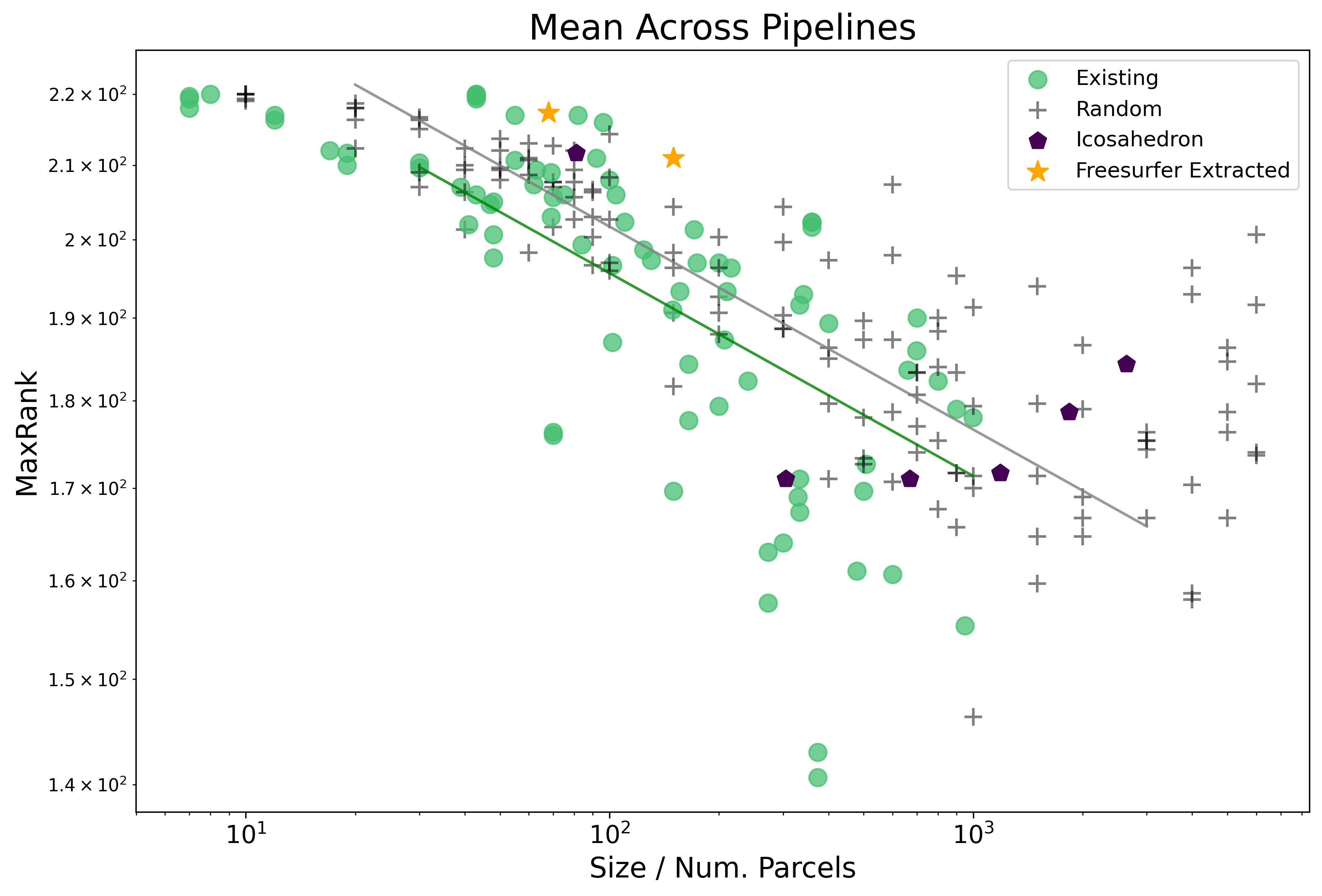
A recreation of the main figure from the index page, but with max rank is provided here:

base

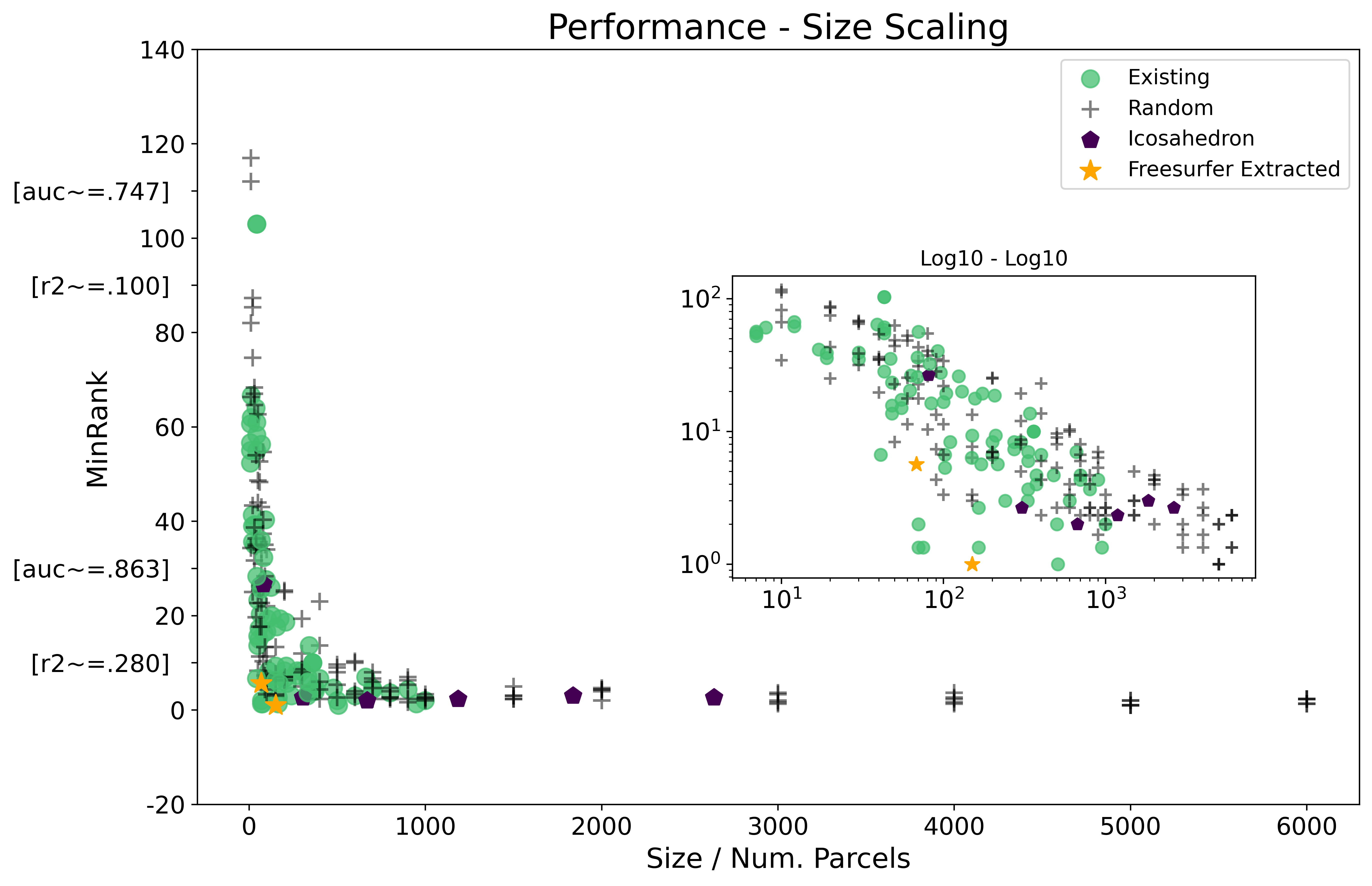
Min Rank

Using Min Rank is similarly different to Mean and Median like Max Rank, but describes the best case performance.

OLS Regression Results
Dep. Variable: Min_Rank R-squared: 0.659
Model: OLS Adj. R-squared: 0.652
Method: Least Squares F-statistic: 91.42
Date: Tue, 11 Jan 2022 Prob (F-statistic): 4.13e-43

coef std err t P>|t| [0.025 0.975]
Intercept 2.5413 0.087 29.240 0.000 2.370 2.713
C(Parcellation_Type)[T.Freesurfer Extracted] -0.7463 0.216 -3.457 0.001 -1.172 -0.320
C(Parcellation_Type)[T.Icosahedron] -0.0231 0.141 -0.164 0.870 -0.301 0.255
C(Parcellation_Type)[T.Random] 0.1130 0.045 2.513 0.013 0.024 0.202
Size -0.7076 0.038 -18.553 0.000 -0.783 -0.632

To match the plot above, and to limit the complexity of the plot, we just show fits for existing and random type parcellations.

fits

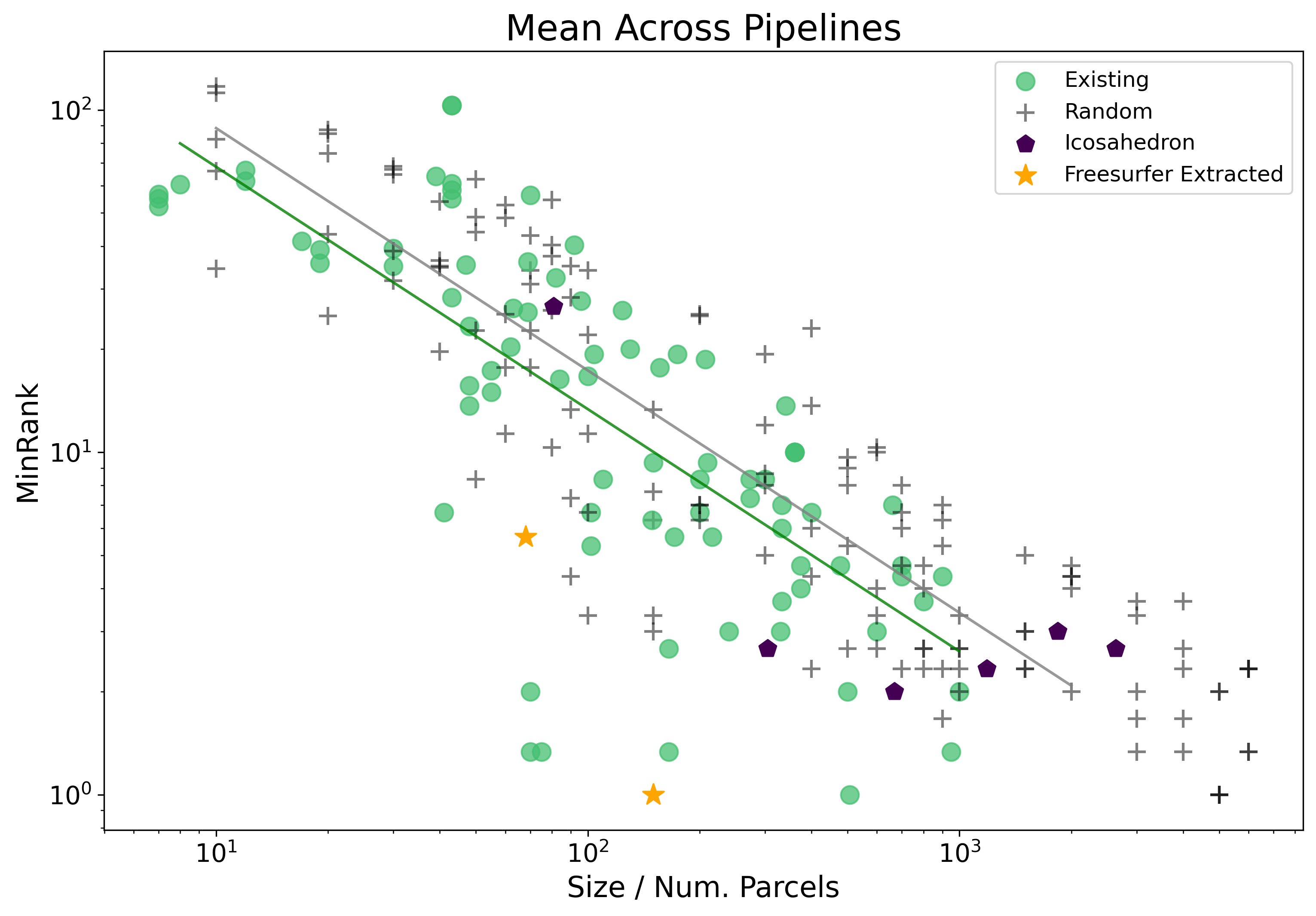
A recreation of the main figure from the index page, but with min rank is provided here:

base