How does front-end univariate feature selection influence scaling?

One reasonable question to ask when comparing the results of the SVM and Elastic-Net pipelines, for example, is to wonder if the SVM’s better scaling (i.e., the Elastic-Net stop showing improvement to performance at a lower number of parcels relative to the SVM) is a result of the front-end feature selection built into the SVM See ML Pipelines.

Elastic-Net FS

To answer this, we can compare the base Elastic-Net pipeline (see Elastic-Net) to a modified version, Elastic-Net FS (feature selection) where a front-end feature selection step is added, simmilar to how the SVM pipeline is setup. Specifically,

Elastic-Net FS BPt Code:

    from BPt import CVStrategy, CV, ParamSearch, Model

    cv_strat = CVStrategy(groups='rel_family_id')

    base_param_search =\
        ParamSearch(search_type='RandomSearch',
                    n_iter=60,
                    cv=CV(splits=3, n_repeats=1, cv_strategy=cv_strat))

    base_model = Model('elastic',
                        params=1,
                        tol=1e-3,
                        max_iter=1000)

    nested_elastic_pipe = Pipeline(steps=feat_selectors + [base_model],
                                   param_search=base_param_search)
 
    model = Model(nested_elastic_pipe)

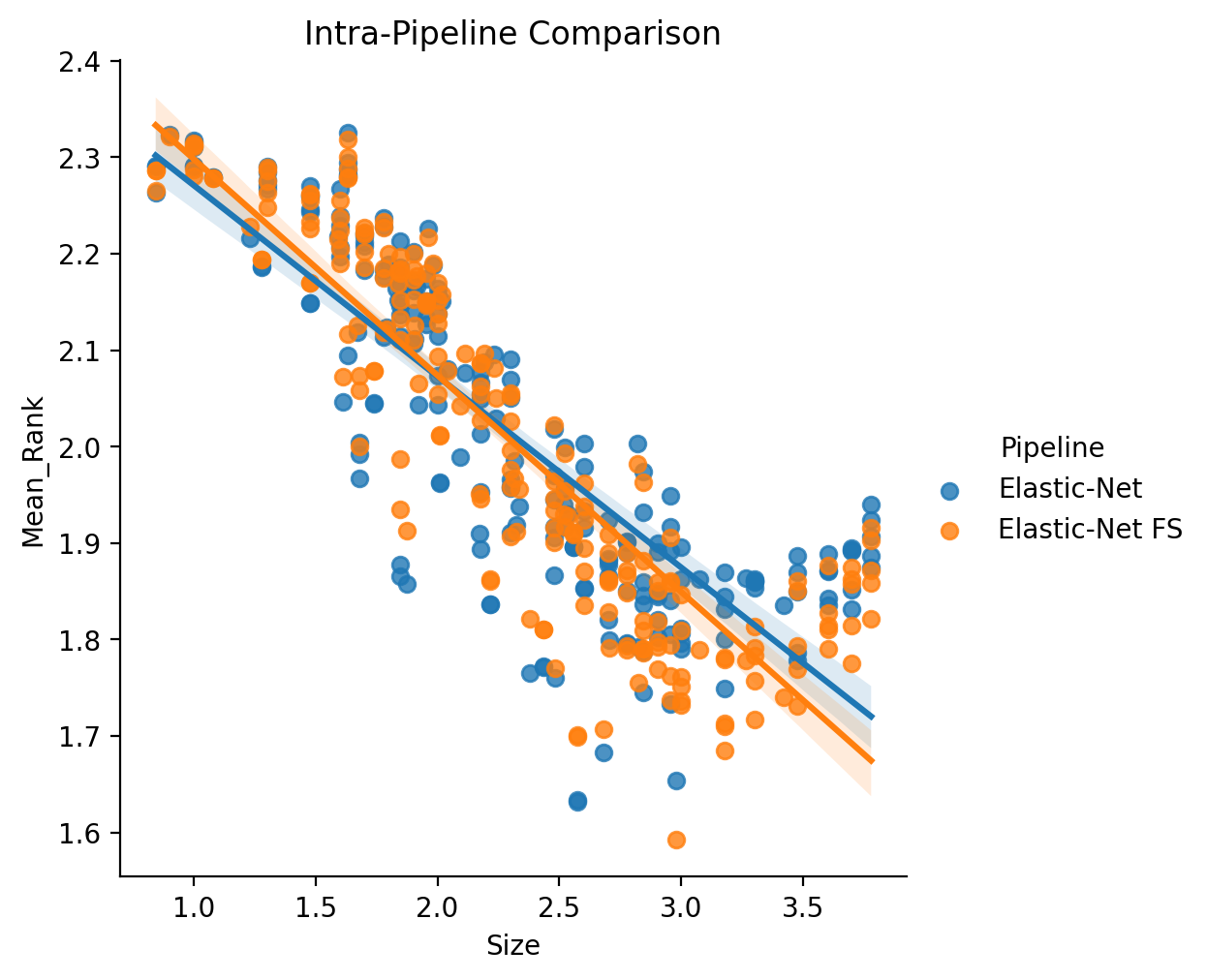
Elastic-Net vs. Elastic-Net FS (Intra-Pipeline)

We compare here the two pipeline in an intra-pipeline fashion, essentially comparing the patterns of scaling between the two pipelines. First, we consider an un-thresholded version (i.e., without first estimating the powerlaw region then truncating). This comparison is notably limited to only the parcellations from the base results. The statistical models fit are of the form: log10(Mean_Rank) ~ log10(Size) + C(Pipeline).

OLS Regression Results

Dep. Variable:	Mean_Rank	R-squared:	0.723
Model:	OLS	Adj. R-squared:	0.722
Method:	Least Squares	F-statistic:	568.3
Date:	Mon, 11 Oct 2021	Prob (F-statistic):	4.64e-122

	coef	std err	t	P>|t|	[0.025	0.975]
Intercept	2.4998	0.016	157.356	0.000	2.469	2.531
C(Pipeline)[T.Elastic-Net FS]	-0.0075	0.009	-0.837	0.403	-0.025	0.010
Size	-0.2114	0.006	-33.701	0.000	-0.224	-0.199

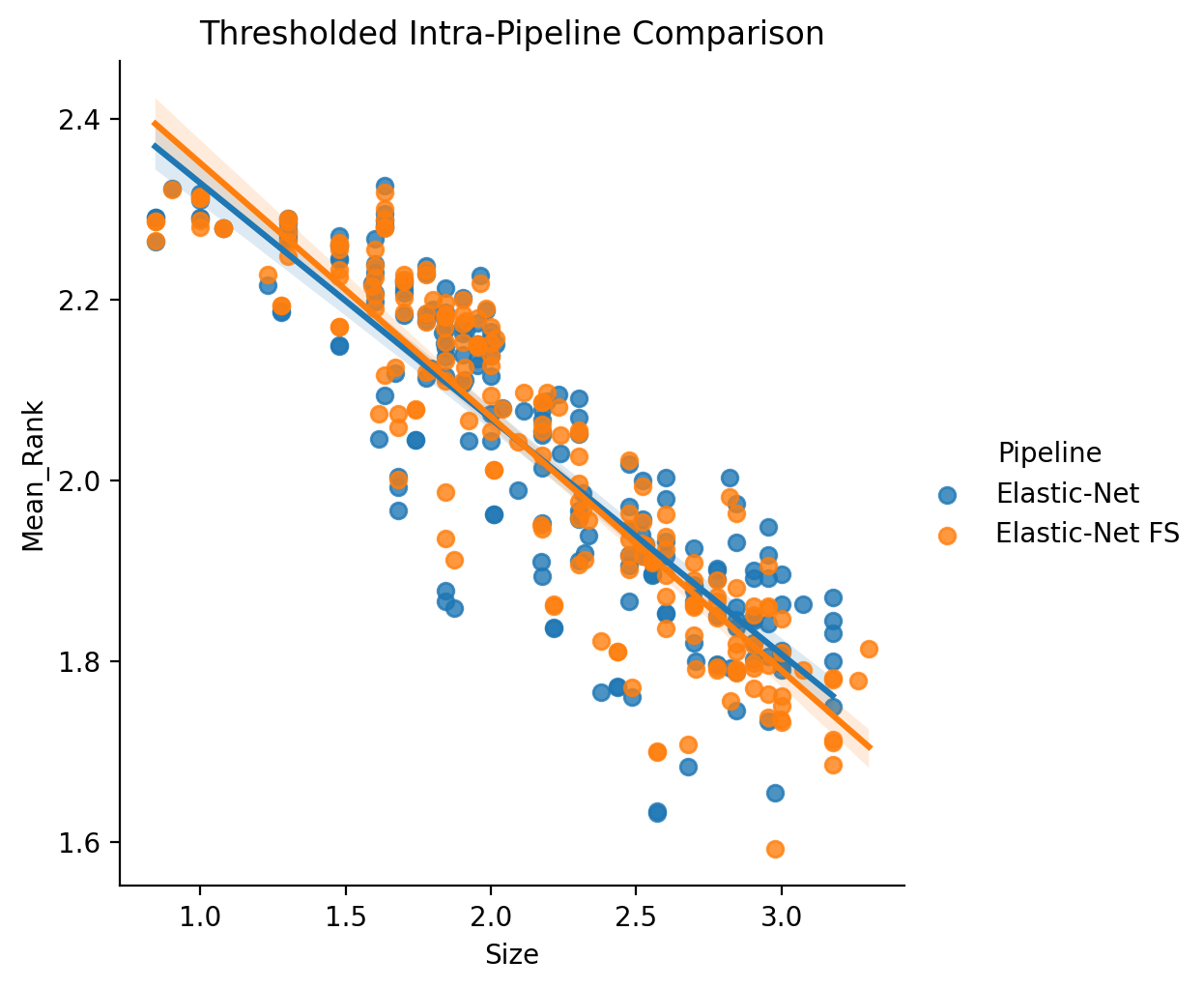
It also may be worthwhile to consider the same version but only within the regions separately estimated to be consistent with powerlaw scaling (See Powerlaw Scaling).

OLS Regression Results

Dep. Variable:	Mean_Rank	R-squared:	0.795
Model:	OLS	Adj. R-squared:	0.794
Method:	Least Squares	F-statistic:	744.2
Date:	Mon, 11 Oct 2021	Prob (F-statistic):	1.15e-132

	coef	std err	t	P>|t|	[0.025	0.975]
Intercept	2.6112	0.016	161.415	0.000	2.579	2.643
C(Pipeline)[T.Elastic-Net FS]	-0.0010	0.008	-0.125	0.900	-0.017	0.015
Size	-0.2708	0.007	-38.576	0.000	-0.285	-0.257

In both cases, regardless of thresholding, we find that scaling remains quite consistent with or without front-end scaling. This implies that the better scaling observed with the SVM results is not due to the impact of the front-end feature selection.

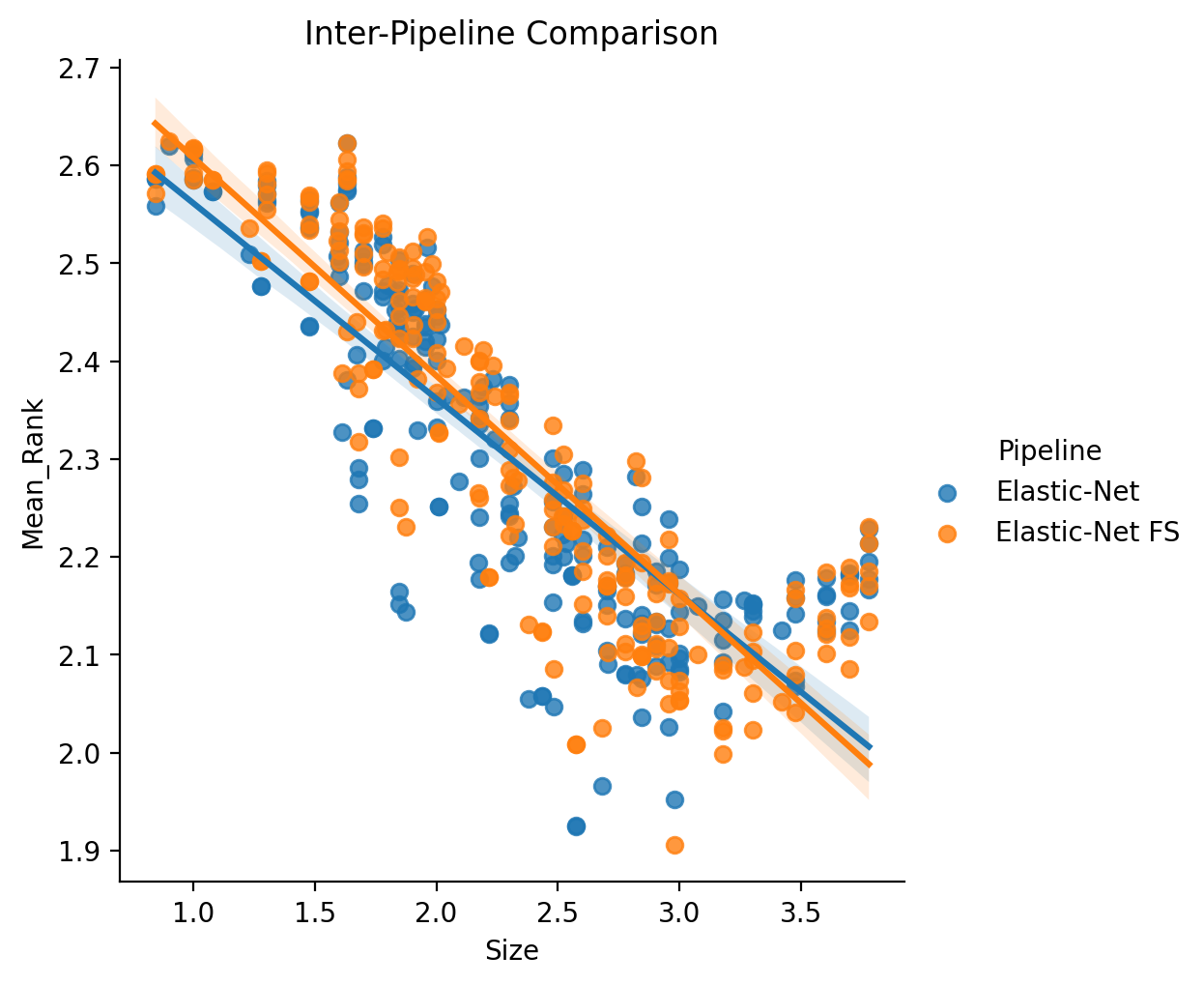
Elastic-Net vs. Elastic-Net FS (Inter-Pipeline)

It is also useful to consider the choice between with front-end feature selection and without in the context of raw performance (i.e., maybe there are no scaling benefits, but is performance improved?). We apply a simmilar statistical model from before, but this time where Mean Rank is derived in an inter-pipeline fashion, formula: log10(Mean_Rank) ~ log10(Size) + C(Pipeline).

OLS Regression Results

Dep. Variable:	Mean_Rank	R-squared:	0.724
Model:	OLS	Adj. R-squared:	0.723
Method:	Least Squares	F-statistic:	570.3
Date:	Mon, 11 Oct 2021	Prob (F-statistic):	2.65e-122

	coef	std err	t	P>|t|	[0.025	0.975]
Intercept	2.7884	0.016	175.557	0.000	2.757	2.820
C(Pipeline)[T.Elastic-Net FS]	0.0158	0.009	1.759	0.079	-0.002	0.033
Size	-0.2115	0.006	-33.731	0.000	-0.224	-0.199

In this case we observe only a very slight, and just barely non significant increase in performance when the nested feature selection is added. In practice, it should not matter which version is used.

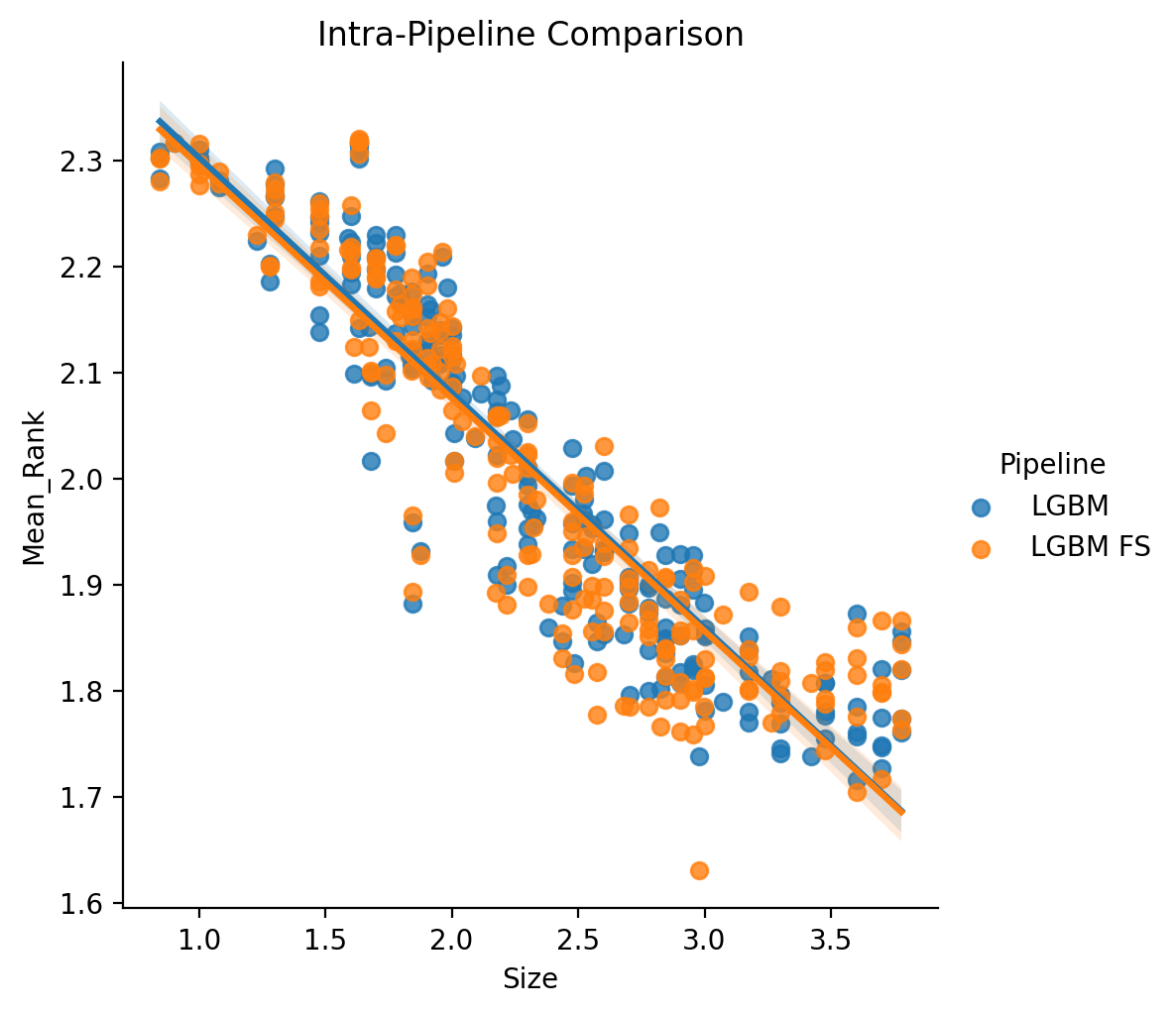
LGBM vs. LGBM FS (Intra-Pipeline)

In the same manner as introduced above, we can consider a version of the LGBM vs. LGBM with front-end feature selection, first in an inter-pipeline un-thresholded manner - with the same statistical model and scope as in the earlier section on Elastic-Net.

OLS Regression Results

Dep. Variable:	Mean_Rank	R-squared:	0.839
Model:	OLS	Adj. R-squared:	0.839
Method:	Least Squares	F-statistic:	1137.
Date:	Mon, 11 Oct 2021	Prob (F-statistic):	1.66e-173

	coef	std err	t	P>|t|	[0.025	0.975]
Intercept	2.5215	0.012	215.270	0.000	2.499	2.545
C(Pipeline)[T.LGBM FS]	-0.0045	0.007	-0.680	0.497	-0.018	0.009
Size	-0.2205	0.005	-47.685	0.000	-0.230	-0.211

Likewise, as before, we consider for completeness, the powerlaw thresholded version (See Powerlaw Scaling).

OLS Regression Results

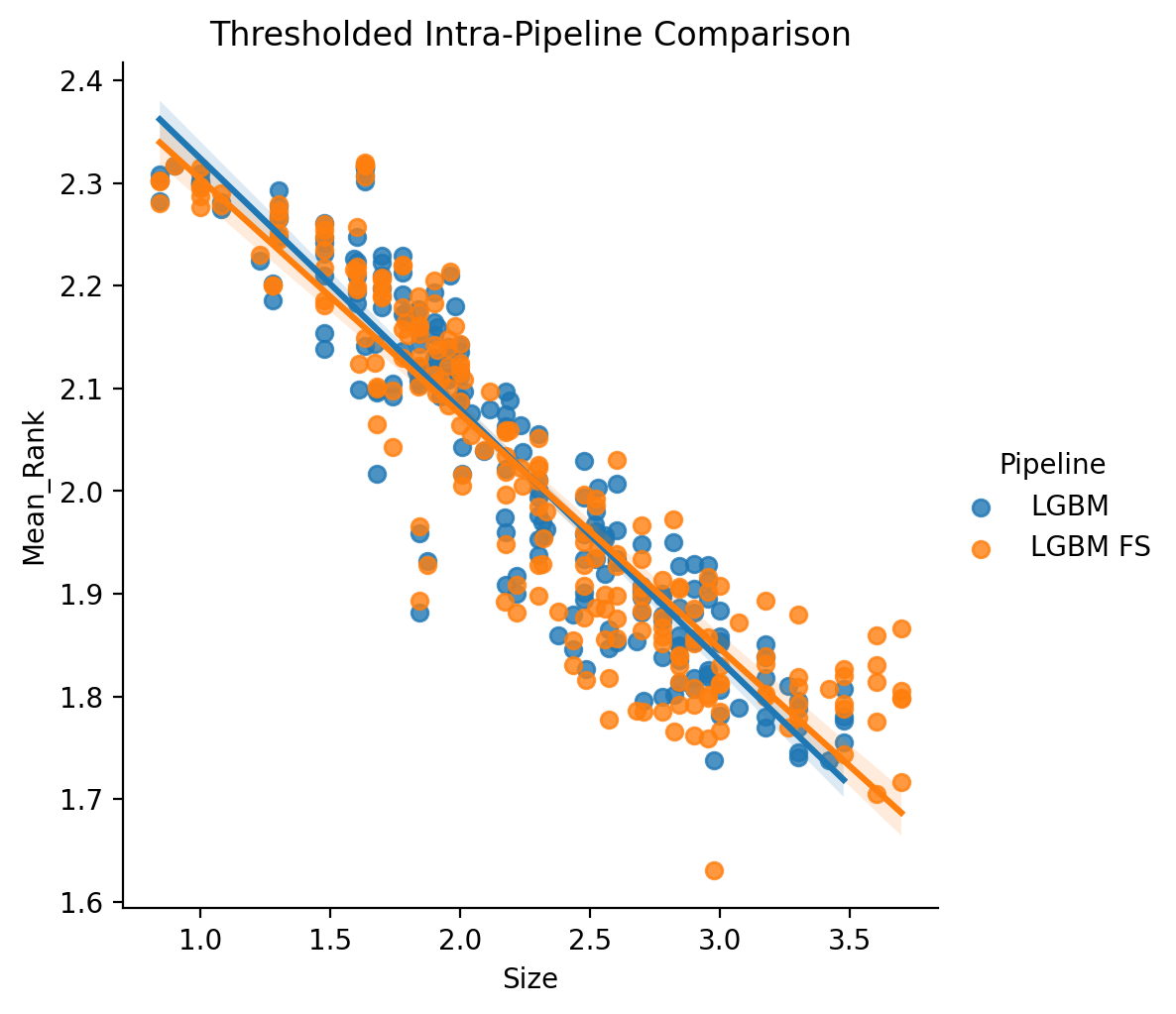
Dep. Variable:	Mean_Rank	R-squared:	0.848
Model:	OLS	Adj. R-squared:	0.848
Method:	Least Squares	F-statistic:	1158.
Date:	Mon, 11 Oct 2021	Prob (F-statistic):	2.62e-170

	coef	std err	t	P>|t|	[0.025	0.975]
Intercept	2.5492	0.012	215.718	0.000	2.526	2.572
C(Pipeline)[T.LGBM FS]	-0.0005	0.007	-0.075	0.940	-0.013	0.012
Size	-0.2357	0.005	-48.048	0.000	-0.245	-0.226

As before with the Elastic-Net based comparison, we find almost identical scaling (actually in this case the difference between the two version might even be smaller than before).

LGBM vs. LGBM FS (Inter-Pipeline)

To complete our comparisons, we last conduct an analysis comparing performance in an inter-pipeline fashion, the same as in the Elastic-Net vs. Elastic-Net FS (Inter-Pipeline) section, but with an LGBM base classifier.

OLS Regression Results

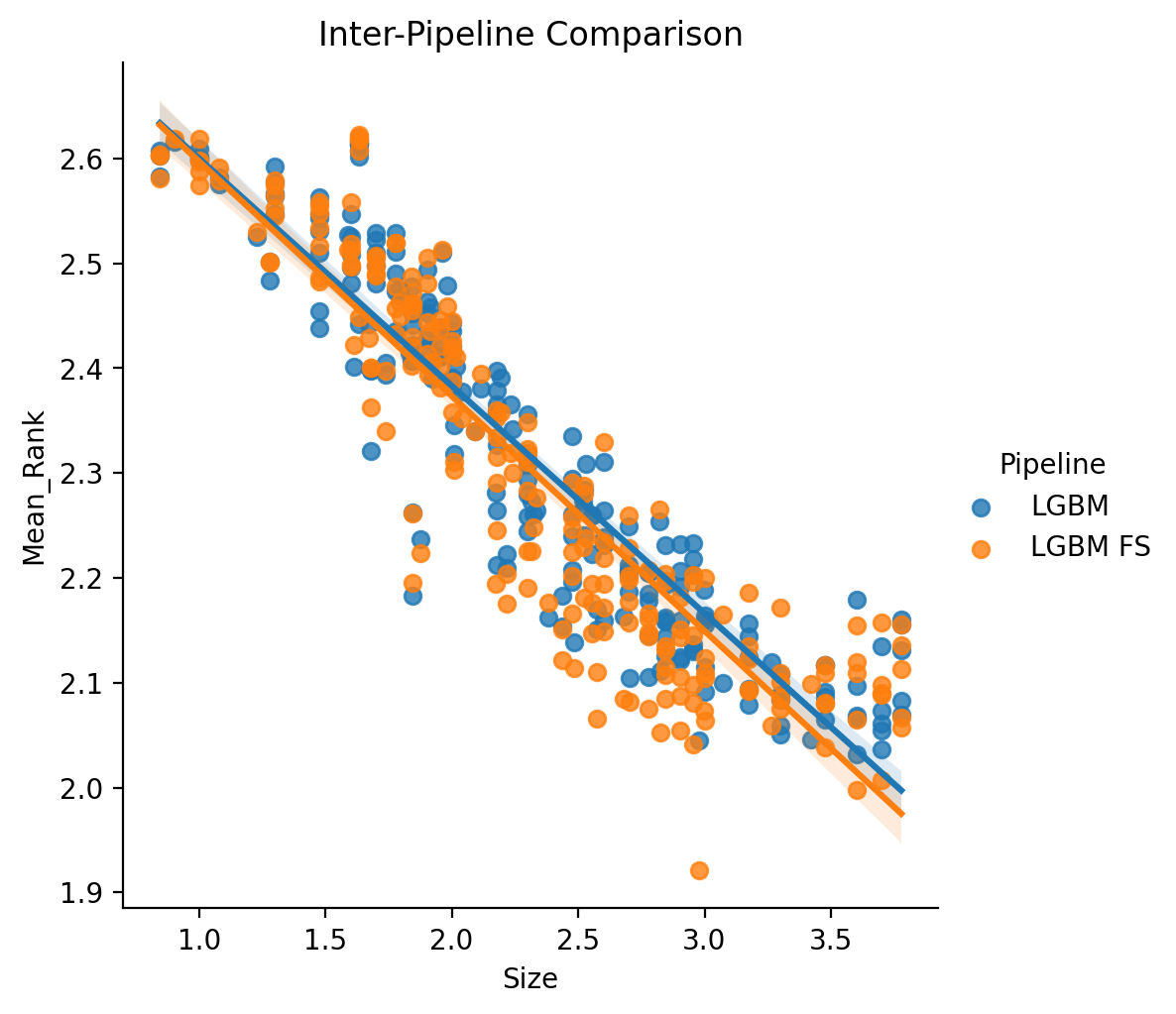
Dep. Variable:	Mean_Rank	R-squared:	0.839
Model:	OLS	Adj. R-squared:	0.839
Method:	Least Squares	F-statistic:	1138.
Date:	Mon, 11 Oct 2021	Prob (F-statistic):	1.57e-173

	coef	std err	t	P>|t|	[0.025	0.975]
Intercept	2.8252	0.012	241.125	0.000	2.802	2.848
C(Pipeline)[T.LGBM FS]	-0.0121	0.007	-1.819	0.070	-0.025	0.001
Size	-0.2204	0.005	-47.660	0.000	-0.230	-0.211

As with the Elastic-Net, any difference in performance is quite minimal - with maybe in both cases a slight, slight tendency towards higher performance with the nested feature selection stage, a difference which is trending towards significant, but not quite.

Conclusion

We can therefore conclude that the unique scaling behavior exhibited by the SVM based pipelines is not the result of a front-end feature scaling. In practice, the choice to include the front-end scaling step can be an easy way to speed up training times (and maybe slightly improve performance) at the expense of a bit of added complexity in construction and description of the underlying pipeline.