Grid vs Random

Given the Results by Target we know that not one scale of parcellation is going to perform best at all scales (i.e., more parcels isn’t always better). It therefore seems intuitively like performing a hyper-parameter search over different random parcellations across a range of scales would be a successful strategy. Likewise, even with a search over fixed scale random parcellations we would expect to be able to atleast do better than just a random parcellation at that same size. Is this the behavior we end up seeing though? Not quite…

In the below plot we plot only the subset of random parcellations between sizes 100 and 1200 along with the results from the ‘Grid’ multiple parcellation strategy.

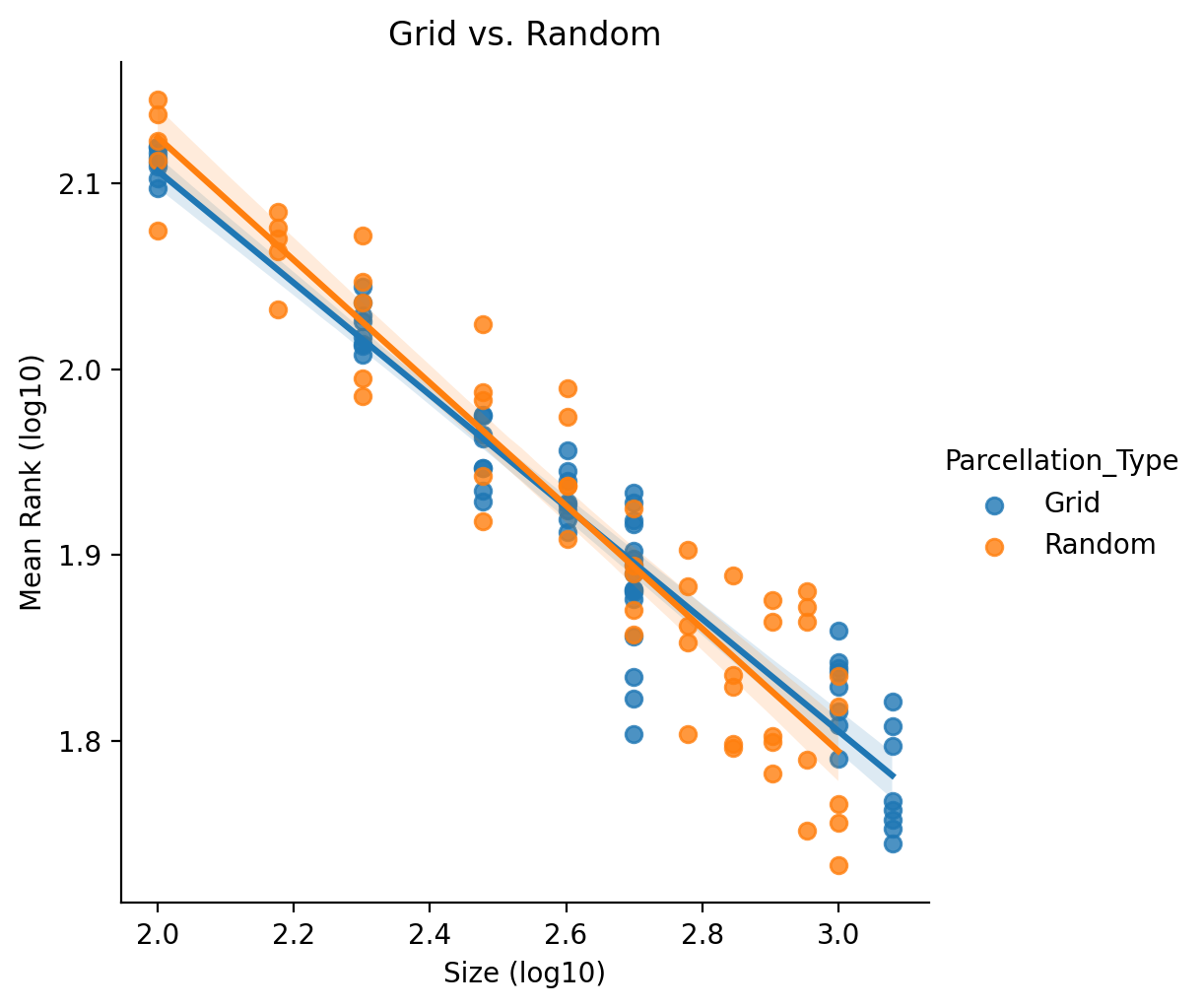
Note that the ‘Size’ for the Grid multiple parcellation strategy is simply set to be the largest single parcellation within the pool of parcellations.

We can also formalize the comparison by modelling these same subsets of data points as: log10(Mean_Rank) ~ log10(Size) * C(Parcellation_Type)

OLS Regression Results

Dep. Variable:	Mean_Rank	R-squared:	0.916
Model:	OLS	Adj. R-squared:	0.914
Method:	Least Squares	F-statistic:	418.0
Date:	Mon, 13 Sep 2021	Prob (F-statistic):	1.15e-61

	coef	std err	t	P>|t|	[0.025	0.975]
Intercept	2.7096	0.031	86.434	0.000	2.648	2.772
C(Parcellation_Type)[T.Random]	0.0758	0.047	1.613	0.109	-0.017	0.169
Size	-0.3014	0.012	-25.270	0.000	-0.325	-0.278
Size:C(Parcellation_Type)[T.Random]	-0.0289	0.018	-1.616	0.109	-0.064	0.007

Even if we treat parcellation type as a fixed effect, the coef. is not significant. Ultimately we find that that searching over multiple parcellations is not a very effective strategy, especially when compared against the ensemble based multiple parcellation strategies. This may relate to a fundamental observed trait in improving ML performance where tuning hyper-parameters typically is not as efficient as ensembling over multiple estimators.