Single vs. Ensembled Parcellations

We can model the results from the Multiple Parcellations Experiment with a focus on teasing apart performance differences between single vs. ensembled parcellations. Specifically we create a binary flag for any results which were ensembled (in this case treating “Grid” as not ensembled), and model as: log10(Mean_Rank) ~ log10(Size) * Is_Ensemble.

OLS Regression Results
Dep. Variable: Mean_Rank R-squared: 0.959
Model: OLS Adj. R-squared: 0.959
Method: Least Squares F-statistic: 3211.
Date: Mon, 13 Sep 2021 Prob (F-statistic): 2.50e-283

coef std err t P>|t| [0.025 0.975]
Intercept 2.7859 0.011 248.940 0.000 2.764 2.808
C(Is_Ensemble)[T.1] 0.6148 0.046 13.348 0.000 0.524 0.705
Size -0.1635 0.005 -36.167 0.000 -0.172 -0.155
Size:C(Is_Ensemble)[T.1] -0.2809 0.014 -19.696 0.000 -0.309 -0.253

The difference is even more obvious when explicitly plotted.

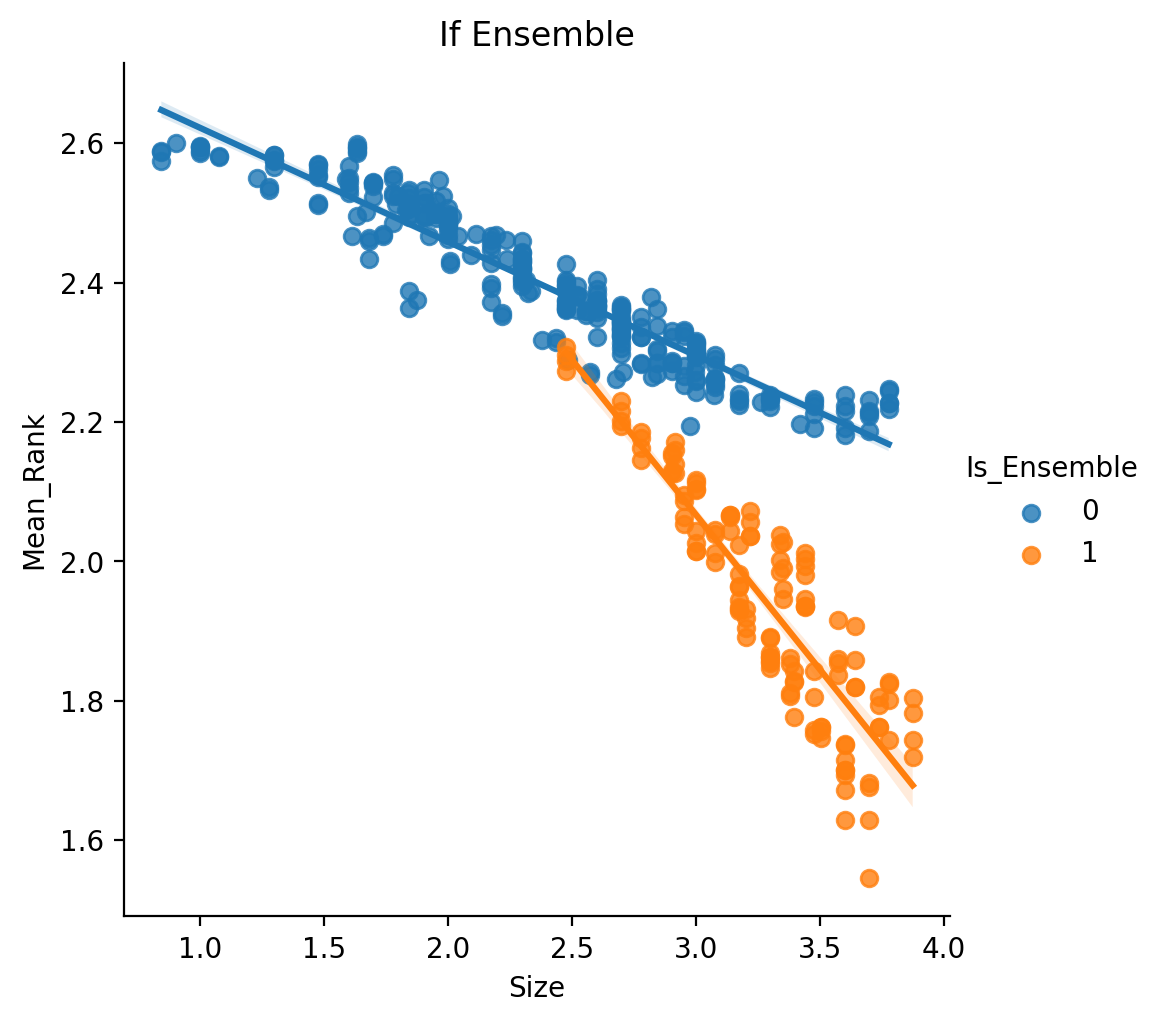
Is Ensemble

The take-away here is that there is a clear benefit in employing ensembles across multiple parcellations especially relative to using the information from a single parcellation. This benefit importantly takes into account that most of the tested ensemble methods have more unique parcels than their single parcellation counterparts. The other point of interest is that these ensembles were all generated using random parcellations, which previous results showed to be much worse than existing parcellations - which serves to highlight even further the benefit from ensembling.

See Also