Results by Parcellation Type
Parcellation Type As Fixed Effect
To model the base results with respect to type of parcellation we use an OLS regression, with
the formula log10(Mean_Rank) ~ log10(Size) + C(Parcellation_Type), so notably first treating choice of parcellation as a fixed effect.
We first though estimate the region where a powerlaw holds and only model the results within this range.
| Dep. Variable: | Mean_Rank | R-squared: | 0.901 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.899 |
| Method: | Least Squares | F-statistic: | 459.6 |
| Date: | Tue, 11 Jan 2022 | Prob (F-statistic): | 6.68e-100 |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 2.6119 | 0.015 | 171.406 | 0.000 | 2.582 | 2.642 |
| C(Parcellation_Type)[T.Freesurfer Extracted] | 0.0154 | 0.042 | 0.367 | 0.714 | -0.067 | 0.098 |
| C(Parcellation_Type)[T.Icosahedron] | -0.0040 | 0.025 | -0.159 | 0.874 | -0.054 | 0.046 |
| C(Parcellation_Type)[T.Random] | 0.0485 | 0.009 | 5.597 | 0.000 | 0.031 | 0.066 |
| Size | -0.2774 | 0.007 | -41.980 | 0.000 | -0.290 | -0.264 |
We note here the significant coef. between existing and random parcellations - we plot below just these two lines of fit, as estimated by the OLS, and colored by parcellation type.
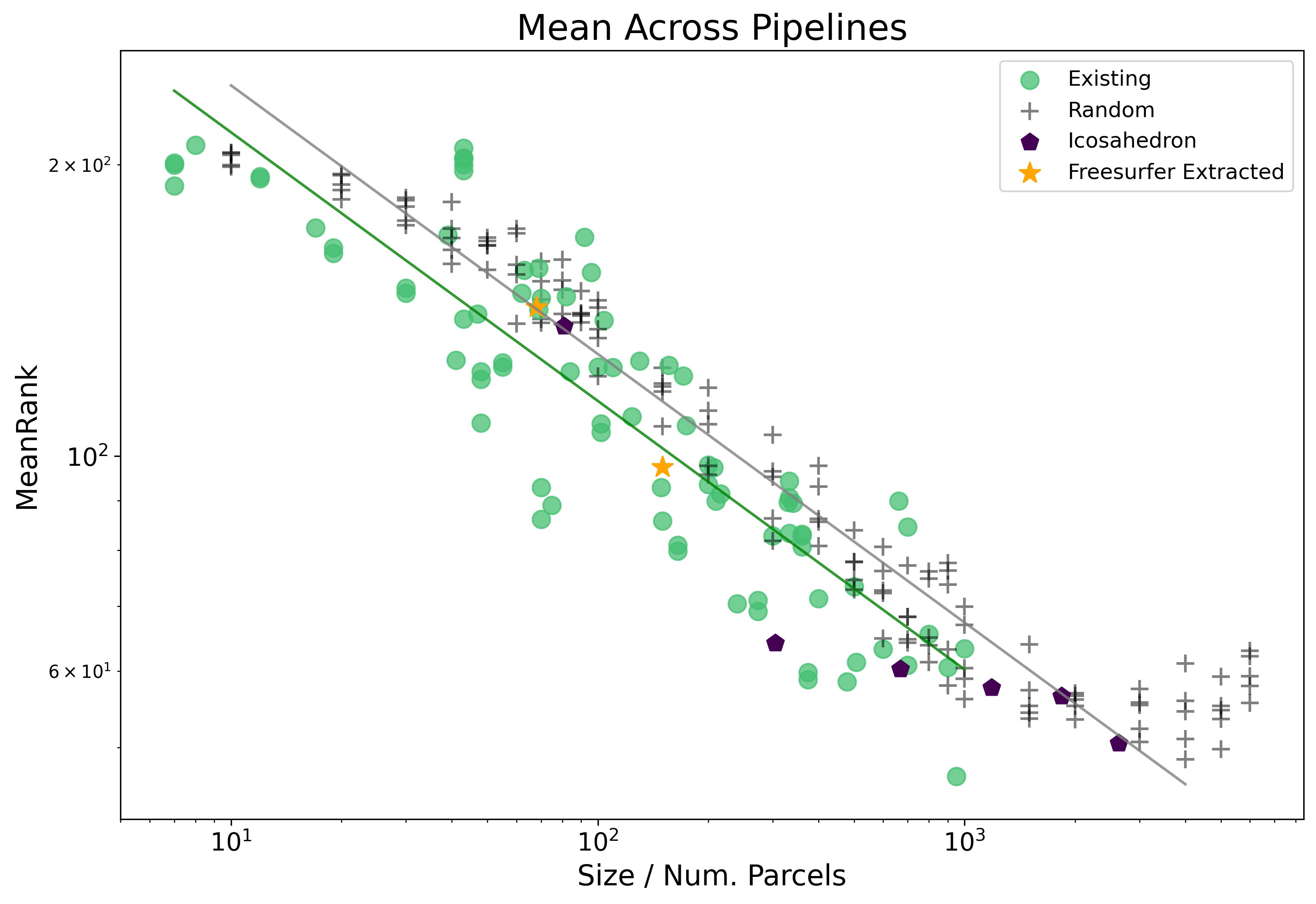
Is it problematic that we only have random parcellations with over 3,000 parcels? No, but see here for a more detailed look.
An additional page recreating this results according to Alternative Ranks is also provided here.
Parcellation Type As Interaction
We can also alternately model parcellation type as as both a fixed effect and with a possible interaction with Size.
| Dep. Variable: | Mean_Rank | R-squared: | 0.894 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.891 |
| Method: | Least Squares | F-statistic: | 255.7 |
| Date: | Mon, 03 Jan 2022 | Prob (F-statistic): | 1.18e-99 |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 2.6026 | 0.028 | 94.524 | 0.000 | 2.548 | 2.657 |
| C(Parcellation_Type)[T.Freesurfer Extracted] | 0.4333 | 0.522 | 0.831 | 0.407 | -0.595 | 1.462 |
| C(Parcellation_Type)[T.Icosahedron] | -0.0614 | 0.147 | -0.418 | 0.677 | -0.352 | 0.229 |
| C(Parcellation_Type)[T.Random] | 0.0049 | 0.033 | 0.149 | 0.882 | -0.061 | 0.070 |
| Size | -0.2739 | 0.013 | -21.097 | 0.000 | -0.299 | -0.248 |
| Size:C(Parcellation_Type)[T.Freesurfer Extracted] | -0.2074 | 0.259 | -0.800 | 0.425 | -0.719 | 0.304 |
| Size:C(Parcellation_Type)[T.Icosahedron] | 0.0201 | 0.052 | 0.386 | 0.700 | -0.082 | 0.122 |
| Size:C(Parcellation_Type)[T.Random] | 0.0226 | 0.015 | 1.521 | 0.130 | -0.007 | 0.052 |
We see that in this case none of the interactions with Size are significant.
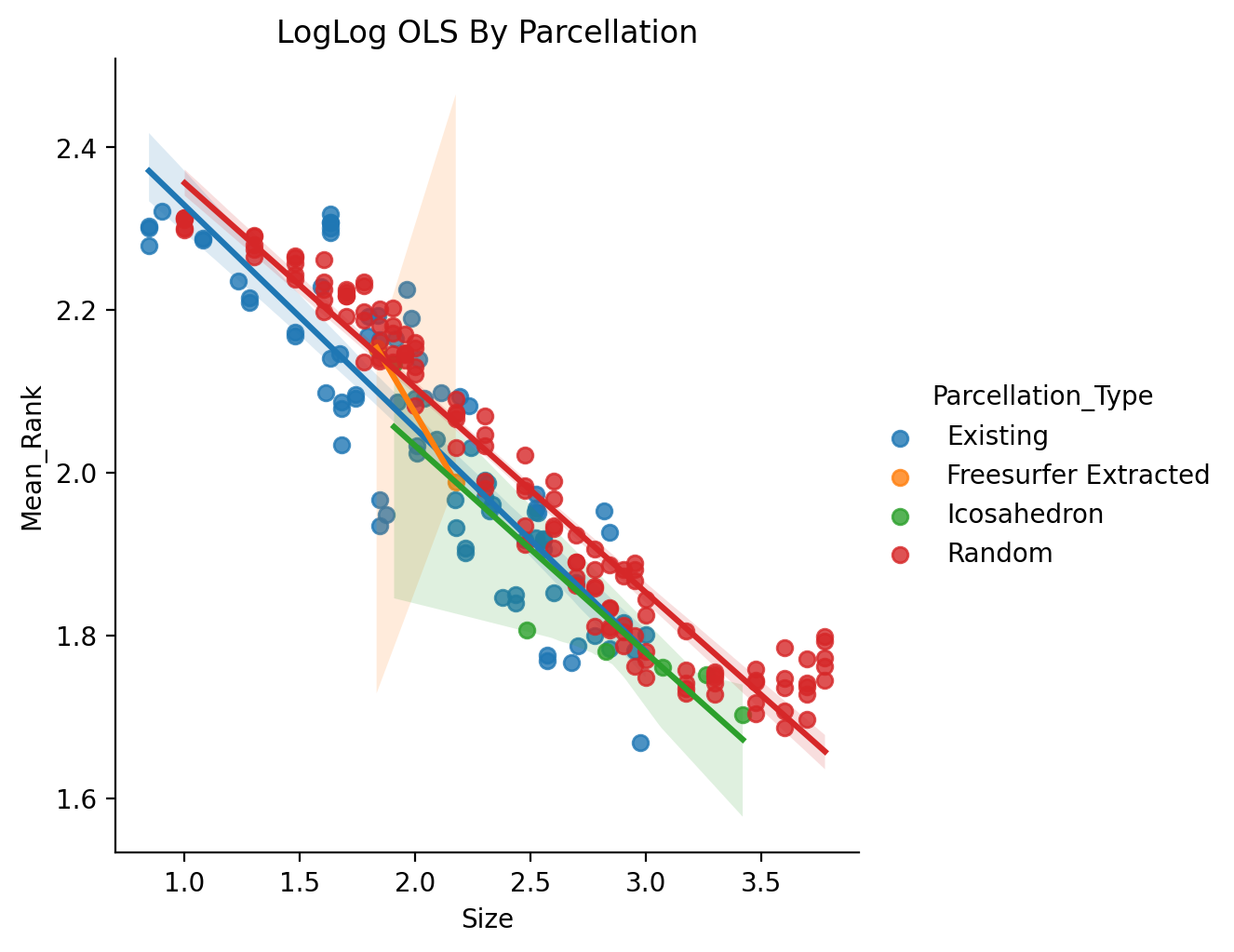
Plotting the basic fits by parcellation type we can see that for parcellations types with only a few samples it is difficult to conclude anything as the sample size is not sufficient.
A key point of interest beyond comparing between parcellation type is the coef. for Size. This represents the scaling exponent in a powerlaw relationship between Size and Performance. We see that despite the choice of how we model parcellation type, this estimated coef. stays fairly stable. Lastly, exploring the interactive plot may be useful seeing how any one parcellation did.
Parcellation Type by Raw Metric
What happens when we look at the results separately for regression and binary targets, according to their respective raw metrics? Note that because we are limiting each analyses to one problem type, the results shown are averaged over less target variables (22 / 23).
Keep in mind also when interpreting the below results that it is fundamentally flawed to look at the raw metrics directly! These results should therefore not be considered as standalone results, see Mean Rank for a description on why this occurs.
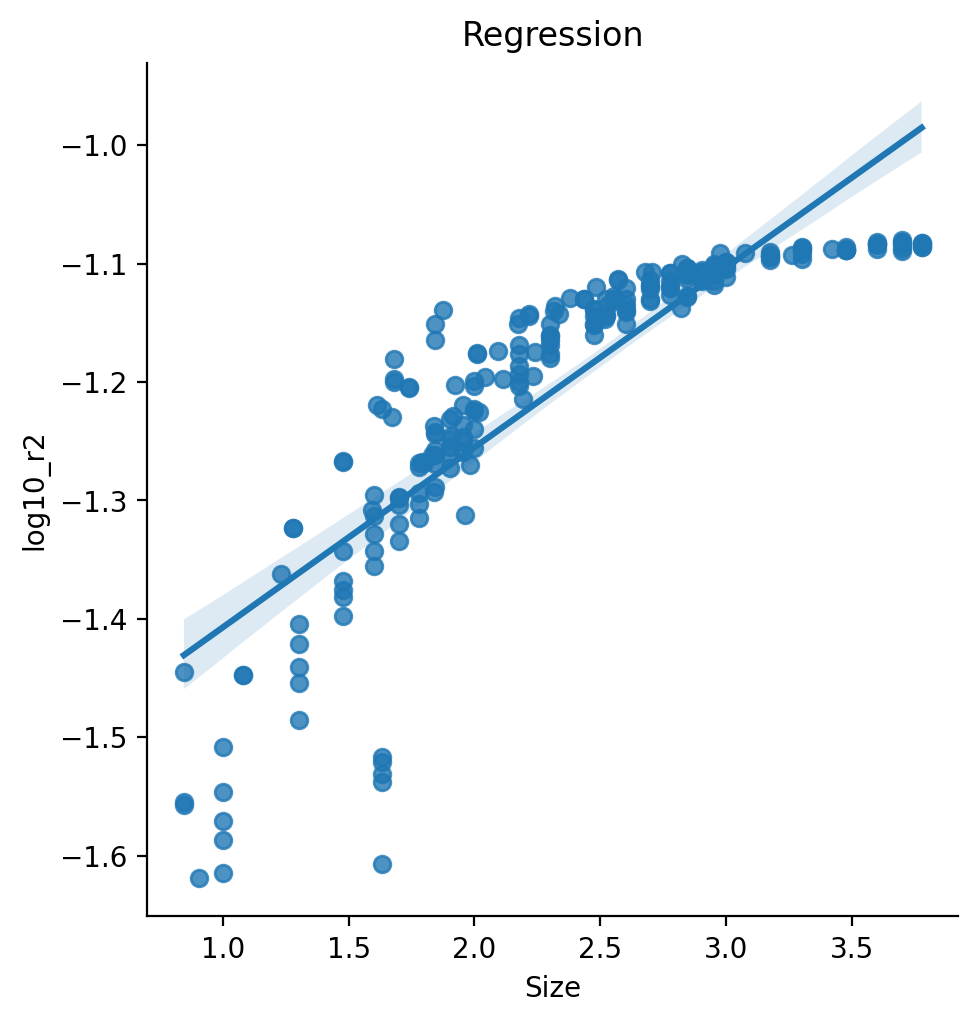
Regression
An Interactive plot by parcellation type as plotted according to R2 values can be found here.
| Dep. Variable: | log10_r2 | R-squared: | 0.747 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.742 |
| Method: | Least Squares | F-statistic: | 158.3 |
| Date: | Tue, 11 Jan 2022 | Prob (F-statistic): | 6.78e-63 |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -1.5528 | 0.015 | -103.261 | 0.000 | -1.582 | -1.523 |
| C(Parcellation_Type)[T.Freesurfer Extracted] | 0.0176 | 0.047 | 0.379 | 0.705 | -0.074 | 0.109 |
| C(Parcellation_Type)[T.Icosahedron] | -0.0216 | 0.028 | -0.773 | 0.440 | -0.077 | 0.033 |
| C(Parcellation_Type)[T.Random] | -0.0400 | 0.010 | -4.178 | 0.000 | -0.059 | -0.021 |
| Size | 0.1596 | 0.006 | 24.782 | 0.000 | 0.147 | 0.172 |
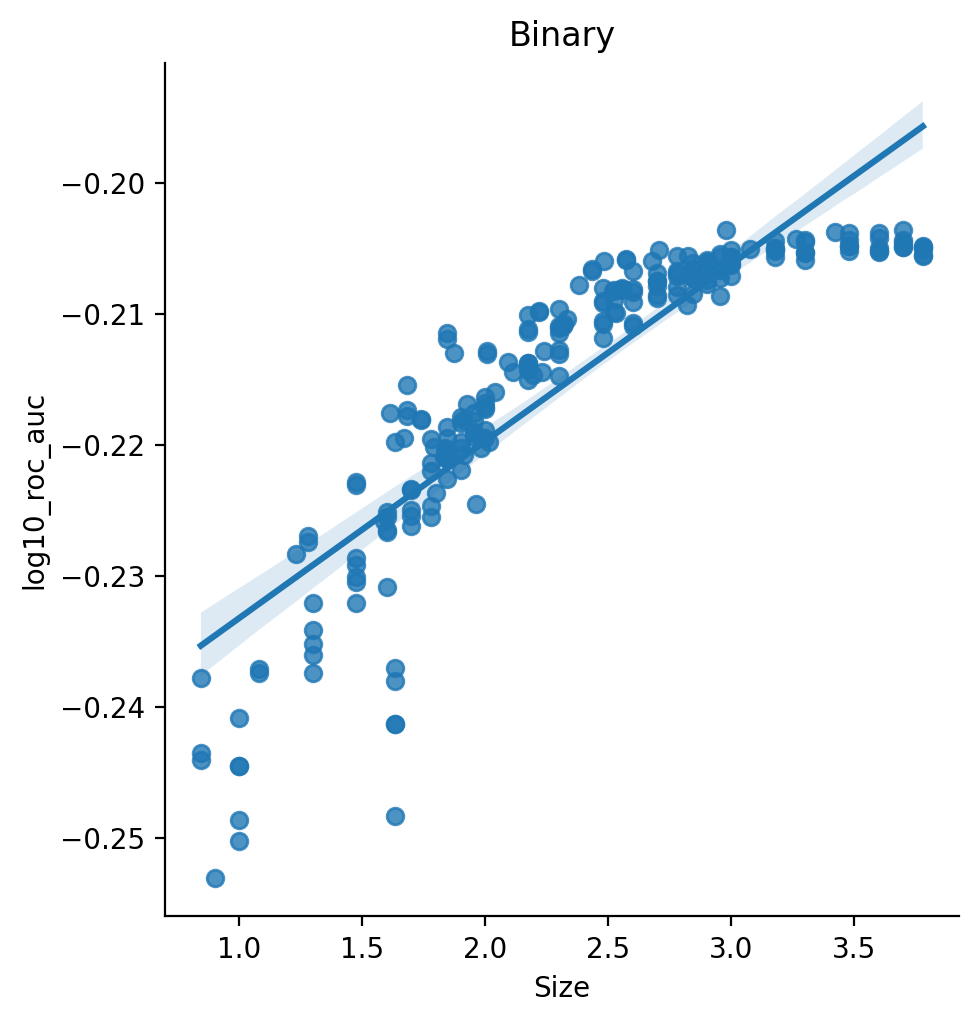
Binary
An Interactive plot by parcellation type as plotted according to ROC AUC values can be found here.
| Dep. Variable: | log10_roc_auc | R-squared: | 0.784 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.780 |
| Method: | Least Squares | F-statistic: | 195.6 |
| Date: | Tue, 11 Jan 2022 | Prob (F-statistic): | 1.94e-70 |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -0.2462 | 0.001 | -204.755 | 0.000 | -0.249 | -0.244 |
| C(Parcellation_Type)[T.Freesurfer Extracted] | 0.0017 | 0.004 | 0.456 | 0.649 | -0.006 | 0.009 |
| C(Parcellation_Type)[T.Icosahedron] | -0.0009 | 0.002 | -0.422 | 0.673 | -0.005 | 0.003 |
| C(Parcellation_Type)[T.Random] | -0.0034 | 0.001 | -4.425 | 0.000 | -0.005 | -0.002 |
| Size | 0.0141 | 0.001 | 27.468 | 0.000 | 0.013 | 0.015 |
Results Table
The table below includes all parcellations specific scores. Notably these are mean relative rankings as averaged across both target variables and ML pipelines. Mean R2 and ROC AUC are calculated only from their relevant subsets of 22 and 23 target variables respectively. Warning: Mean R2 and ROC AUC should be taken with a grain of salt due to scaling issues between different targets.
Table columns are sortable!
| Parcellation | Mean Rank | Size | Mean R2 | Mean ROC AUC | Median Rank |
|---|---|---|---|---|---|
| difumo 1024 | 46.7037 | 949 | 0.0811 | 0.6257 | 34.6667 |
| random 4000 1 | 48.6148 | 4000 | 0.0823 | 0.6254 | 35.6667 |
| random 5000 2 | 49.8000 | 5000 | 0.0832 | 0.6258 | 32.3333 |
| icosahedron 1442 (dlab) | 50.5111 | 2637 | 0.0817 | 0.6255 | 39.3333 |
| random 3000 1 | 50.6741 | 3000 | 0.0820 | 0.6254 | 40.0000 |
| random 4000 0 | 51.0519 | 4000 | 0.0826 | 0.6249 | 34.3333 |
| random 3000 2 | 52.2741 | 3000 | 0.0815 | 0.6246 | 42.0000 |
| random 2000 4 | 53.4519 | 2000 | 0.0809 | 0.6247 | 48.0000 |
| random 5000 4 | 53.5407 | 5000 | 0.0825 | 0.6239 | 40.6667 |
| random 1500 3 | 53.5778 | 1500 | 0.0813 | 0.6234 | 40.6667 |
| random 1500 4 | 54.3333 | 1500 | 0.0808 | 0.6237 | 41.0000 |
| random 4000 2 | 54.5259 | 4000 | 0.0829 | 0.6234 | 43.6667 |
| random 5000 3 | 54.6519 | 5000 | 0.0820 | 0.6246 | 39.0000 |
| random 5000 0 | 55.2000 | 5000 | 0.0828 | 0.6239 | 43.3333 |
| random 1500 0 | 55.2074 | 1500 | 0.0806 | 0.6246 | 41.3333 |
| random 2000 1 | 55.2444 | 2000 | 0.0802 | 0.6244 | 47.3333 |
| random 3000 4 | 55.3037 | 3000 | 0.0816 | 0.6240 | 43.6667 |
| random 6000 1 | 55.6222 | 6000 | 0.0824 | 0.6239 | 43.6667 |
| random 3000 3 | 55.6741 | 3000 | 0.0816 | 0.6240 | 44.6667 |
| random 4000 3 | 55.8889 | 4000 | 0.0825 | 0.6238 | 39.0000 |
| random 2000 0 | 56.0593 | 2000 | 0.0819 | 0.6232 | 43.6667 |
| random 1000 4 | 56.1333 | 1000 | 0.0794 | 0.6235 | 48.3333 |
| icosahedron 1002 (dlab) | 56.5037 | 1838 | 0.0808 | 0.6247 | 48.0000 |
| random 2000 2 | 56.5481 | 2000 | 0.0820 | 0.6225 | 40.3333 |
| random 2000 3 | 56.9259 | 2000 | 0.0816 | 0.6233 | 43.3333 |
| random 1500 1 | 57.3037 | 1500 | 0.0805 | 0.6238 | 47.3333 |
| random 3000 0 | 57.4741 | 3000 | 0.0816 | 0.6235 | 44.3333 |
| icosahedron 642 (dlab) | 57.6741 | 1186 | 0.0811 | 0.6237 | 47.0000 |
| random 6000 2 | 57.8889 | 6000 | 0.0827 | 0.6240 | 42.0000 |
| random 900 1 | 57.9704 | 900 | 0.0794 | 0.6215 | 49.3333 |
| difumo 512 | 58.4667 | 478 | 0.0782 | 0.6223 | 56.3333 |
| mist 444 | 58.7704 | 374 | 0.0771 | 0.6226 | 54.3333 |
| random 1000 2 | 58.9185 | 1000 | 0.0797 | 0.6228 | 54.0000 |
| random 5000 1 | 59.1926 | 5000 | 0.0814 | 0.6243 | 39.0000 |
| random 6000 0 | 59.2519 | 6000 | 0.0827 | 0.6237 | 55.6667 |
| basc scale444 | 59.7926 | 374 | 0.0769 | 0.6225 | 55.0000 |
| icosahedron 362 (dlab) | 60.3111 | 669 | 0.0793 | 0.6229 | 53.6667 |
| random 1000 0 | 60.4148 | 1000 | 0.0790 | 0.6228 | 50.0000 |
| schaefer 900 | 60.5259 | 900 | 0.0790 | 0.6231 | 49.6667 |
| schaefer 700 | 60.8444 | 700 | 0.0788 | 0.6221 | 48.0000 |
| random 4000 4 | 61.0519 | 4000 | 0.0817 | 0.6234 | 50.6667 |
| random 800 4 | 61.2741 | 800 | 0.0776 | 0.6222 | 55.0000 |
| sjh | 61.2889 | 507 | 0.0782 | 0.6235 | 54.3333 |
| random 6000 3 | 62.1185 | 6000 | 0.0821 | 0.6229 | 54.3333 |
| random 6000 4 | 62.9407 | 6000 | 0.0821 | 0.6230 | 49.6667 |
| random 900 0 | 63.1333 | 900 | 0.0778 | 0.6228 | 54.3333 |
| schaefer 600 | 63.2296 | 600 | 0.0780 | 0.6229 | 59.3333 |
| schaefer 1000 | 63.2963 | 998 | 0.0797 | 0.6221 | 53.6667 |
| random 800 3 | 63.7852 | 800 | 0.0781 | 0.6215 | 56.0000 |
| random 1500 2 | 63.9407 | 1500 | 0.0800 | 0.6228 | 50.3333 |
| icosahedron 162 (dlab) | 64.0963 | 305 | 0.0759 | 0.6224 | 59.0000 |
| random 700 0 | 64.2000 | 700 | 0.0787 | 0.6204 | 57.6667 |
| random 700 4 | 64.7111 | 700 | 0.0777 | 0.6214 | 57.3333 |
| random 600 2 | 64.8000 | 600 | 0.0780 | 0.6213 | 62.3333 |
| random 800 2 | 64.9333 | 800 | 0.0782 | 0.6225 | 55.0000 |
| schaefer 800 | 65.4963 | 800 | 0.0784 | 0.6223 | 53.6667 |
| random 1000 3 | 66.9481 | 1000 | 0.0774 | 0.6219 | 65.0000 |
| random 700 1 | 68.2444 | 700 | 0.0778 | 0.6215 | 63.0000 |
| random 700 2 | 68.2741 | 700 | 0.0772 | 0.6206 | 63.3333 |
| mist 325 | 69.1630 | 273 | 0.0741 | 0.6214 | 68.3333 |
| random 1000 1 | 69.9185 | 1000 | 0.0787 | 0.6207 | 59.0000 |
| difumo 256 | 70.4074 | 240 | 0.0743 | 0.6197 | 68.0000 |
| basc scale325 | 70.9778 | 273 | 0.0742 | 0.6213 | 69.6667 |
| schaefer 400 | 71.2667 | 400 | 0.0757 | 0.6212 | 68.0000 |
| random 600 1 | 72.2444 | 600 | 0.0767 | 0.6195 | 65.0000 |
| random 600 0 | 72.6889 | 600 | 0.0760 | 0.6207 | 67.6667 |
| random 500 1 | 72.7704 | 500 | 0.0770 | 0.6186 | 69.3333 |
| schaefer 500 | 73.3481 | 500 | 0.0762 | 0.6211 | 67.6667 |
| random 900 3 | 73.6889 | 900 | 0.0768 | 0.6205 | 69.0000 |
| random 500 2 | 74.4741 | 500 | 0.0760 | 0.6201 | 72.3333 |
| random 800 0 | 74.7556 | 800 | 0.0768 | 0.6203 | 67.6667 |
| random 800 1 | 76.0444 | 800 | 0.0771 | 0.6198 | 69.3333 |
| random 600 3 | 76.0889 | 600 | 0.0748 | 0.6210 | 76.3333 |
| random 900 2 | 76.1778 | 900 | 0.0762 | 0.6214 | 68.0000 |
| random 700 3 | 77.1481 | 700 | 0.0745 | 0.6206 | 73.6667 |
| random 900 4 | 77.5852 | 900 | 0.0783 | 0.6186 | 65.3333 |
| random 500 4 | 77.7556 | 500 | 0.0756 | 0.6183 | 77.0000 |
| random 500 0 | 77.8296 | 500 | 0.0738 | 0.6202 | 79.3333 |
| basc scale197 | 79.8370 | 165 | 0.0720 | 0.6169 | 82.6667 |
| random 600 4 | 80.6074 | 600 | 0.0758 | 0.6187 | 75.0000 |
| glasser (abox) | 80.6148 | 360 | 0.0746 | 0.6193 | 78.0000 |
| random 400 4 | 80.8000 | 400 | 0.0742 | 0.6193 | 81.6667 |
| mist 197 | 80.9037 | 165 | 0.0717 | 0.6168 | 82.6667 |
| random 300 0 | 81.7556 | 300 | 0.0727 | 0.6180 | 80.3333 |
| schaefer 300 | 82.7185 | 300 | 0.0726 | 0.6194 | 83.3333 |
| glasser 2016 (dlab) | 82.7481 | 360 | 0.0740 | 0.6194 | 76.3333 |
| hcp mmp | 83.1259 | 360 | 0.0741 | 0.6192 | 77.0000 |
| gordon (abox) | 83.2963 | 333 | 0.0742 | 0.6192 | 82.6667 |
| random 500 3 | 83.8593 | 500 | 0.0741 | 0.6196 | 85.3333 |
| Slab1068 | 84.5556 | 699 | 0.0746 | 0.6188 | 80.3333 |
| random 400 1 | 85.5259 | 400 | 0.0734 | 0.6179 | 90.0000 |
| destrieux (abox) | 85.7259 | 150 | 0.0714 | 0.6164 | 92.3333 |
| smith rsn70 | 86.0741 | 70 | 0.0706 | 0.6146 | 94.0000 |
| random 400 2 | 86.2000 | 400 | 0.0726 | 0.6190 | 86.0000 |
| random 300 4 | 86.2148 | 300 | 0.0717 | 0.6178 | 92.6667 |
| allen | 88.9704 | 75 | 0.0726 | 0.6123 | 90.0000 |
| aicha | 89.4074 | 341 | 0.0734 | 0.6167 | 87.0000 |
| shen 368 | 89.6000 | 330 | 0.0713 | 0.6190 | 89.6667 |
| fan (abox) | 89.8519 | 210 | 0.0732 | 0.6155 | 89.3333 |
| Slab907 | 89.8593 | 661 | 0.0729 | 0.6176 | 87.6667 |
| CAPRSC | 90.6370 | 333 | 0.0719 | 0.6180 | 91.3333 |
| brainnetome | 91.4741 | 216 | 0.0720 | 0.6160 | 93.0000 |
| smith bm70 | 92.8148 | 70 | 0.0685 | 0.6139 | 105.0000 |
| dextrieux (dlab) | 92.8519 | 149 | 0.0706 | 0.6150 | 99.6667 |
| random 400 3 | 93.0296 | 400 | 0.0723 | 0.6156 | 94.0000 |
| shen (abox) | 93.5111 | 200 | 0.0707 | 0.6172 | 98.0000 |
| gordon | 94.2963 | 333 | 0.0717 | 0.6168 | 92.0000 |
| random 300 3 | 95.2370 | 300 | 0.0705 | 0.6155 | 96.3333 |
| random 200 3 | 95.7333 | 200 | 0.0690 | 0.6145 | 101.6667 |
| random 300 1 | 96.4370 | 300 | 0.0706 | 0.6158 | 96.0000 |
| shen 268 | 97.3259 | 207 | 0.0724 | 0.6153 | 94.3333 |
| freesurfer destr | 97.4222 | 150 | 0.0677 | 0.6146 | 100.6667 |
| random 400 0 | 97.7037 | 400 | 0.0706 | 0.6152 | 94.3333 |
| random 200 1 | 97.7185 | 200 | 0.0685 | 0.6151 | 108.0000 |
| schaefer 200 | 97.9259 | 200 | 0.0692 | 0.6153 | 102.3333 |
| random 300 2 | 105.2444 | 300 | 0.0691 | 0.6140 | 109.3333 |
| basc scale122 | 105.8815 | 102 | 0.0668 | 0.6123 | 111.3333 |
| random 150 3 | 107.3481 | 150 | 0.0666 | 0.6113 | 118.3333 |
| CPAC200 | 107.5481 | 174 | 0.0668 | 0.6126 | 112.0000 |
| random 200 2 | 107.9333 | 200 | 0.0678 | 0.6127 | 112.0000 |
| mist 122 | 107.9852 | 102 | 0.0666 | 0.6126 | 114.0000 |
| harvard oxford cort 1mm | 108.1778 | 48 | 0.0660 | 0.6090 | 114.6667 |
| difumo 128 | 109.9111 | 124 | 0.0670 | 0.6114 | 111.0000 |
| random 200 4 | 111.4148 | 200 | 0.0667 | 0.6123 | 111.6667 |
| random 150 0 | 116.6296 | 150 | 0.0631 | 0.6113 | 128.3333 |
| random 200 0 | 117.6667 | 200 | 0.0661 | 0.6099 | 120.3333 |
| random 150 4 | 118.0889 | 150 | 0.0651 | 0.6109 | 125.6667 |
| random 150 2 | 118.8889 | 150 | 0.0641 | 0.6106 | 125.0000 |
| harvard oxford cort maxprob thr25 1mm | 120.0741 | 48 | 0.0631 | 0.6062 | 129.3333 |
| random 100 4 | 120.8963 | 100 | 0.0626 | 0.6070 | 131.0000 |
| baldassano (abox) | 121.0444 | 171 | 0.0638 | 0.6103 | 125.6667 |
| aal | 122.3037 | 84 | 0.0627 | 0.6069 | 131.0000 |
| harvard oxford cort maxprob thr0 1mm | 122.3185 | 48 | 0.0635 | 0.6056 | 131.0000 |
| random 150 1 | 123.3704 | 150 | 0.0626 | 0.6094 | 131.3333 |
| MICCAI | 123.5333 | 110 | 0.0637 | 0.6082 | 129.0000 |
| mist 64 | 123.6815 | 55 | 0.0625 | 0.6052 | 133.0000 |
| schaefer 100 | 123.6815 | 100 | 0.0632 | 0.6076 | 130.3333 |
| nspn500 | 124.0889 | 156 | 0.0611 | 0.6100 | 131.3333 |
| basc scale064 | 124.9481 | 55 | 0.0623 | 0.6053 | 133.0000 |
| power (abox) | 125.3630 | 130 | 0.0635 | 0.6103 | 128.6667 |
| brodmann | 125.6741 | 41 | 0.0604 | 0.6059 | 141.0000 |
| random 100 2 | 132.4370 | 100 | 0.0597 | 0.6066 | 137.6667 |
| random 100 0 | 135.2444 | 100 | 0.0599 | 0.6064 | 139.3333 |
| icosahedron 42 (dlab) | 136.1778 | 81 | 0.0568 | 0.6052 | 149.3333 |
| random 80 3 | 136.9037 | 80 | 0.0587 | 0.6049 | 144.6667 |
| random 60 2 | 137.0000 | 60 | 0.0539 | 0.6032 | 158.6667 |
| random 70 3 | 137.3630 | 70 | 0.0572 | 0.6045 | 147.0000 |
| random 90 0 | 137.4667 | 90 | 0.0561 | 0.6060 | 150.3333 |
| vdg11b | 138.1704 | 104 | 0.0595 | 0.6028 | 145.3333 |
| random 70 2 | 138.5259 | 70 | 0.0547 | 0.6033 | 148.6667 |
| economo | 138.5259 | 43 | 0.0599 | 0.6029 | 147.0000 |
| random 90 4 | 139.6889 | 90 | 0.0603 | 0.6051 | 145.6667 |
| harvard oxford cort maxprob thr50 1mm | 140.2074 | 47 | 0.0590 | 0.6033 | 147.3333 |
| random 90 2 | 140.2222 | 90 | 0.0567 | 0.6038 | 151.6667 |
| random 80 0 | 140.3185 | 80 | 0.0565 | 0.6055 | 152.6667 |
| random 90 3 | 140.5037 | 90 | 0.0581 | 0.6040 | 148.3333 |
| desikan (dlab) | 141.6444 | 69 | 0.0579 | 0.6022 | 152.3333 |
| random 100 1 | 142.3778 | 100 | 0.0555 | 0.6033 | 156.6667 |
| freesurfer desikan | 142.5630 | 68 | 0.0547 | 0.6013 | 152.6667 |
| random 100 3 | 144.8444 | 100 | 0.0576 | 0.6041 | 151.0000 |
| random 70 0 | 145.2296 | 70 | 0.0538 | 0.6020 | 160.0000 |
| desikan (abox) | 145.6593 | 70 | 0.0570 | 0.6018 | 152.6667 |
| aal (abox) | 146.1704 | 82 | 0.0591 | 0.6015 | 149.3333 |
| mist 36 | 147.3333 | 30 | 0.0542 | 0.5986 | 162.3333 |
| difumo 64 | 147.3556 | 62 | 0.0540 | 0.6023 | 155.6667 |
| random 90 1 | 148.0519 | 90 | 0.0551 | 0.6034 | 155.6667 |
| random 80 2 | 148.5852 | 80 | 0.0548 | 0.6028 | 159.3333 |
| basc scale036 | 149.1037 | 30 | 0.0540 | 0.5983 | 163.3333 |
| random 70 4 | 151.5630 | 70 | 0.0553 | 0.6011 | 161.3333 |
| random 80 1 | 151.9037 | 80 | 0.0534 | 0.6022 | 163.3333 |
| random 60 3 | 154.0222 | 60 | 0.0535 | 0.6006 | 161.6667 |
| yeo (abox) | 154.8963 | 96 | 0.0537 | 0.6022 | 162.6667 |
| Hammersmith | 155.6370 | 63 | 0.0539 | 0.5975 | 164.6667 |
| random 50 2 | 155.8074 | 50 | 0.0503 | 0.5978 | 173.0000 |
| power2011 (dlab) | 156.3481 | 69 | 0.0510 | 0.6016 | 168.0000 |
| random 60 0 | 157.6444 | 60 | 0.0508 | 0.5997 | 168.6667 |
| random 40 3 | 157.9333 | 40 | 0.0506 | 0.5955 | 172.3333 |
| random 70 1 | 159.0000 | 70 | 0.0514 | 0.5990 | 170.3333 |
| random 80 4 | 159.6444 | 80 | 0.0556 | 0.5999 | 169.0000 |
| basc scale020 | 162.0296 | 19 | 0.0475 | 0.5930 | 178.6667 |
| random 40 2 | 163.3556 | 40 | 0.0486 | 0.5949 | 179.0000 |
| mist 20 | 164.0963 | 19 | 0.0475 | 0.5924 | 179.3333 |
| random 50 1 | 165.0741 | 50 | 0.0478 | 0.5979 | 180.3333 |
| random 50 3 | 165.2222 | 50 | 0.0505 | 0.5957 | 175.0000 |
| random 50 4 | 166.8889 | 50 | 0.0497 | 0.5940 | 178.0000 |
| random 40 0 | 167.9852 | 40 | 0.0470 | 0.5934 | 182.3333 |
| random 50 0 | 168.1407 | 50 | 0.0463 | 0.5950 | 181.3333 |
| Juelich | 168.3185 | 92 | 0.0487 | 0.5964 | 178.0000 |
| msdl | 169.2889 | 39 | 0.0492 | 0.5945 | 177.6667 |
| random 60 4 | 169.9556 | 60 | 0.0484 | 0.5950 | 177.6667 |
| random 60 1 | 171.8370 | 60 | 0.0498 | 0.5961 | 178.0000 |
| random 40 1 | 171.8593 | 40 | 0.0454 | 0.5936 | 186.0000 |
| yeo 17networks | 172.1852 | 17 | 0.0434 | 0.5912 | 187.6667 |
| random 30 3 | 173.1481 | 30 | 0.0428 | 0.5907 | 187.3333 |
| random 30 2 | 175.1852 | 30 | 0.0454 | 0.5900 | 188.3333 |
| random 30 4 | 181.0000 | 30 | 0.0415 | 0.5888 | 194.6667 |
| random 40 4 | 183.0000 | 40 | 0.0441 | 0.5877 | 191.0000 |
| random 30 0 | 183.7333 | 30 | 0.0421 | 0.5860 | 194.0000 |
| random 20 3 | 184.1704 | 20 | 0.0394 | 0.5861 | 198.0000 |
| random 30 1 | 185.0074 | 30 | 0.0400 | 0.5882 | 197.0000 |
| random 20 0 | 188.3778 | 20 | 0.0379 | 0.5832 | 201.0000 |
| yeo 7networks | 190.1778 | 7 | 0.0359 | 0.5784 | 201.6667 |
| random 20 4 | 190.7481 | 20 | 0.0362 | 0.5789 | 203.3333 |
| mist 12 | 193.4741 | 12 | 0.0357 | 0.5793 | 204.0000 |
| basc scale012 | 194.4741 | 12 | 0.0357 | 0.5789 | 204.0000 |
| random 20 1 | 195.0741 | 20 | 0.0351 | 0.5818 | 202.6667 |
| random 20 2 | 195.7630 | 20 | 0.0327 | 0.5807 | 206.6667 |
| craddock tcorr 2level | 197.3185 | 43 | 0.0304 | 0.5793 | 208.0000 |
| random 10 3 | 199.0963 | 10 | 0.0310 | 0.5744 | 207.6667 |
| random 10 1 | 199.8074 | 10 | 0.0285 | 0.5694 | 212.0000 |
| mist 7 | 199.9259 | 7 | 0.0279 | 0.5708 | 211.3333 |
| craddock tcorr mean | 200.0000 | 43 | 0.0301 | 0.5781 | 208.6667 |
| basc scale007 | 200.8296 | 7 | 0.0277 | 0.5700 | 212.0000 |
| craddock scorr mean | 203.0000 | 43 | 0.0290 | 0.5737 | 211.0000 |
| craddock scorr 2level | 203.2889 | 43 | 0.0295 | 0.5737 | 209.3333 |
| random 10 2 | 204.8148 | 10 | 0.0269 | 0.5695 | 213.0000 |
| random 10 0 | 205.8222 | 10 | 0.0243 | 0.5621 | 216.0000 |
| random 10 4 | 205.8370 | 10 | 0.0259 | 0.5642 | 214.0000 |
| Princetonvisual top | 208.0963 | 43 | 0.0247 | 0.5645 | 214.6667 |
| oasis.chubs | 209.5333 | 8 | 0.0241 | 0.5584 | 216.3333 |