Predict Waist Circumference with Diffusion Weighted Imaging#
This notebook using diffusion weighted imaging data, and subjects waist circumference in cm from the ABCD Study. We will use as input feature derived Restriction spectrum imaging (RSI) from diffusion weighted images. This notebook covers data loading as well as evaluation across a large number of different ML Pipelines. This notebook may be useful for people looking for more examples on what different Pipelines to try.
[1]:
import BPt as bp
import pandas as pd
import os
from warnings import simplefilter
from sklearn.exceptions import ConvergenceWarning
simplefilter("ignore", category=ConvergenceWarning)
Load the data needed#
Data is loaded from a large csv file with all of the features from release 2 of the ABCD study.
[2]:
def load_from_rds(names, eventname='baseline_year_1_arm_1'):
data = pd.read_csv('data/nda_rds_201.csv',
usecols=['src_subject_id', 'eventname'] + names,
na_values=['777', 999, '999', 777])
data = data.loc[data[data['eventname'] == eventname].index]
data = data.set_index('src_subject_id')
data = data.drop('eventname', axis=1)
# Obsificate subject ID for public example
data.index = list(range(len(data)))
# Return as pandas DataFrame cast to BPt Dataset
return bp.Dataset(data)
[3]:
# This way we can look at all column available
all_cols = list(pd.read_csv('data/nda_rds_201.csv', nrows=0))
all_cols[:10]
[3]:
['subjectid',
'src_subject_id',
'eventname',
'anthro_1_height_in',
'anthro_2_height_in',
'anthro_3_height_in',
'anthro_height_calc',
'anthro_weight_cast',
'anthro_weight_a_location',
'anthro_weight1_lb']
[4]:
# The target variable
target_cols = ['anthro_waist_cm']
# non input feature - i.e., those that inform
non_input_cols = ['sex', 'rel_family_id']
# We will use the fiber at dti measures
dti_cols = [c for c in all_cols if '_fiber.at' in c and 'rsi.' in c]
len(dti_cols)
[4]:
294
Now we can use the helper function defined at the start to load these features in as a Dataset
[5]:
data = load_from_rds(target_cols + non_input_cols + dti_cols)
data.shape
[5]:
(11875, 297)
[6]:
# This is optional, but will print out some extra verbosity when using the dataset operations
data.verbose = 1
The first step we will do is tell the dataset what roles the different columns are. See: https://sahahn.github.io/BPt/user_guide/role.html
[7]:
data = data.set_target(target_cols) # Note we doing data = data.func()
data = data.set_non_input(non_input_cols)
data
Dropped 2 Rows
Dropped 6 Rows
[7]:
Data
| dmri_rsi.n0_fiber.at_allfib.lh | dmri_rsi.n0_fiber.at_allfib.rh | dmri_rsi.n0_fiber.at_allfibers | dmri_rsi.n0_fiber.at_allfibnocc.lh | dmri_rsi.n0_fiber.at_allfibnocc.rh | dmri_rsi.n0_fiber.at_atr.lh | dmri_rsi.n0_fiber.at_atr.rh | dmri_rsi.n0_fiber.at_cc | dmri_rsi.n0_fiber.at_cgc.lh | dmri_rsi.n0_fiber.at_cgc.rh | ... | dmri_rsi.vol_fiber.at_scs.lh | dmri_rsi.vol_fiber.at_scs.rh | dmri_rsi.vol_fiber.at_sifc.lh | dmri_rsi.vol_fiber.at_sifc.rh | dmri_rsi.vol_fiber.at_slf.lh | dmri_rsi.vol_fiber.at_slf.rh | dmri_rsi.vol_fiber.at_tslf.lh | dmri_rsi.vol_fiber.at_tslf.rh | dmri_rsi.vol_fiber.at_unc.lh | dmri_rsi.vol_fiber.at_unc.rh | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.327623 | 0.323420 | 0.325957 | 0.340559 | 0.332364 | 0.347837 | 0.336072 | 0.306803 | 0.311347 | 0.304854 | ... | 23672.0 | 13056.0 | 9648.0 | 9528.0 | 10152.0 | 11504.0 | 8384.0 | 8024.0 | 4968.0 | 7176.0 |
| 1 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 2 | 0.325374 | 0.311465 | 0.319027 | 0.341213 | 0.326334 | 0.346651 | 0.335362 | 0.288124 | 0.326416 | 0.300990 | ... | 33112.0 | 19256.0 | 11928.0 | 8688.0 | 13144.0 | 15344.0 | 10488.0 | 10936.0 | 6904.0 | 9480.0 |
| 3 | 0.305095 | 0.304357 | 0.305170 | 0.315477 | 0.312866 | 0.313972 | 0.316729 | 0.288742 | 0.289166 | 0.290347 | ... | 28480.0 | 16016.0 | 13024.0 | 11960.0 | 13600.0 | 14880.0 | 11416.0 | 10592.0 | 6952.0 | 8736.0 |
| 4 | 0.316860 | 0.315238 | 0.316399 | 0.328251 | 0.327259 | 0.333998 | 0.318162 | 0.294008 | 0.297800 | 0.299230 | ... | 29904.0 | 17968.0 | 12720.0 | 11336.0 | 13528.0 | 15672.0 | 11096.0 | 11816.0 | 5912.0 | 7336.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 11870 | 0.335741 | 0.336048 | 0.336372 | 0.349806 | 0.347732 | 0.349966 | 0.345692 | 0.312056 | 0.324054 | 0.336676 | ... | 28328.0 | 15400.0 | 9656.0 | 10080.0 | 11312.0 | 13496.0 | 8728.0 | 9176.0 | 4960.0 | 7392.0 |
| 11871 | 0.320563 | 0.317525 | 0.319429 | 0.327302 | 0.322161 | 0.333086 | 0.315482 | 0.308554 | 0.299938 | 0.298093 | ... | 23792.0 | 13632.0 | 9928.0 | 8912.0 | 9152.0 | 12288.0 | 7128.0 | 8912.0 | 5744.0 | 7376.0 |
| 11872 | 0.327051 | 0.325386 | 0.326522 | 0.340918 | 0.334854 | 0.345435 | 0.335610 | 0.305720 | 0.308630 | 0.330612 | ... | 28640.0 | 16384.0 | 9496.0 | 11216.0 | 12168.0 | 12312.0 | 9520.0 | 8952.0 | 4568.0 | 9056.0 |
| 11873 | 0.323579 | 0.319377 | 0.321805 | 0.334945 | 0.329433 | 0.332200 | 0.334017 | 0.304399 | 0.303831 | 0.307037 | ... | 26216.0 | 14672.0 | 9408.0 | 8872.0 | 10960.0 | 12584.0 | 8880.0 | 9176.0 | 3696.0 | 6168.0 |
| 11874 | 0.383537 | 0.371483 | 0.377822 | 0.394413 | 0.373486 | 0.404684 | 0.374435 | 0.366270 | 0.415342 | 0.418280 | ... | 26544.0 | 15624.0 | 9904.0 | 10360.0 | 9904.0 | 12216.0 | 7712.0 | 8000.0 | 5208.0 | 8816.0 |
11867 rows × 294 columns
Target
| anthro_waist_cm | |
|---|---|
| 0 | 31.00 |
| 1 | 30.50 |
| 2 | 26.75 |
| 3 | 23.50 |
| 4 | 30.00 |
| ... | ... |
| 11870 | 26.00 |
| 11871 | 30.00 |
| 11872 | 19.00 |
| 11873 | 25.00 |
| 11874 | 32.00 |
11867 rows × 1 columns
Non Input
| rel_family_id | sex | |
|---|---|---|
| 0 | 8780.0 | F |
| 1 | 10207.0 | F |
| 2 | 4720.0 | M |
| 3 | 3804.0 | M |
| 4 | 5358.0 | M |
| ... | ... | ... |
| 11870 | 3791.0 | M |
| 11871 | 2441.0 | F |
| 11872 | 7036.0 | F |
| 11873 | 6681.0 | F |
| 11874 | 7588.0 | F |
11867 rows × 2 columns
A few things to note right off the bat.
The verbosity printed us out two statements, about dropping rows. This is due to a constraint on columns of role ‘non input’ that there cannot be any NaN / missing data, so those lines just say 2 NaN’s were found when loading the first non input column and 6 when loading the next.
The values for sex are still ‘F’ and ‘M’, we will handle that next.
Some columns with role data are missing values. We will handle that as well.
[8]:
# We explicitly say this variable should be binary
data.to_binary('sex', inplace=True)
# We will ordinalize rel_family_id too
data = data.ordinalize(scope='rel_family_id')
data['non input']
[8]:
Non Input
| rel_family_id | sex | |
|---|---|---|
| 0 | 7321 | 0 |
| 1 | 8634 | 0 |
| 2 | 3971 | 1 |
| 3 | 3139 | 1 |
| 4 | 4543 | 1 |
| ... | ... | ... |
| 11870 | 3128 | 1 |
| 11871 | 2111 | 0 |
| 11872 | 5907 | 0 |
| 11873 | 5594 | 0 |
| 11874 | 6238 | 0 |
11867 rows × 2 columns
Next let’s look into that NaN problem we saw before.
[9]:
data.nan_info()
Loaded NaN Info:
There are: 332348 total missing values
180 columns found with 1131 missing values (column name overlap: ['dmri_rsi.n', '_fiber.at_'])
66 columns found with 1130 missing values (column name overlap: ['dmri_rsi.n', '_fiber.at_'])
42 columns found with 1128 missing values (column name overlap: ['dmri_rsi.vol_fiber.at_'])
6 columns found with 1133 missing values (column name overlap: ['_fiber.at_cgh.lh', 'dmri_rsi.n'])
Seems like most of the missing data is missing for everyone, i.e., if the above info founds columns with only a few missing values, we might want to do something different, but this tells us that when data is missing it is missing for all columns.
We just drop any subjects with any NaN data below across the target variable and the Data
[10]:
data = data.drop_nan_subjects(scope='all')
Dropped 1145 Rows
Another thing we need to worry about with data like this is corrupted data, i.e., data with values that don’t make sense due to a failure in the automatic processing pipeline. Let’s look at the target variable first, then the data.
[11]:
data.plot('target')
data['target'].max(), data['target'].min(),
anthro_waist_cm: 10722 rows
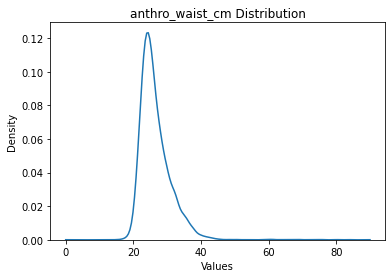
[11]:
(anthro_waist_cm 90.0
dtype: float64,
anthro_waist_cm 0.0
dtype: float64)
Yeah I don’t know about that waist cm of 0 … The below code can be used to try different values of outliers to drop, since it is not by default applied in place.
[12]:
data.filter_outliers_by_std(scope='target', n_std=5).plot('target')
Dropped 33 Rows
anthro_waist_cm: 10689 rows
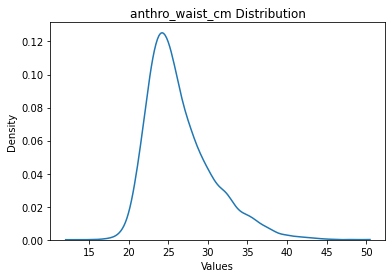
5 std seems okay, so let’s actually apply it.
[13]:
data.filter_outliers_by_std(scope='target', n_std=5, inplace=True)
Dropped 33 Rows
Let’s look at the distribution of skew values for the dti data
[14]:
data['data'].skew().sort_values()
[14]:
dmri_rsi.nd_fiber.at_fmaj -2.420074
dmri_rsi.nds2_fiber.at_fmaj -2.287048
dmri_rsi.nd_fiber.at_cst.lh -2.213900
dmri_rsi.nt_fiber.at_cst.lh -2.198591
dmri_rsi.nds2_fiber.at_fmin -2.101969
...
dmri_rsi.nts2_fiber.at_cst.rh 0.992159
dmri_rsi.n0s2_fiber.at_fmin 1.005677
dmri_rsi.nts2_fiber.at_fmin 1.006378
dmri_rsi.n0s2_fiber.at_cst.lh 1.072836
dmri_rsi.nts2_fiber.at_cst.lh 1.090904
Length: 294, dtype: float64
Looks okay, let’s choose the variable with the most extreme skew to plot.
[15]:
data.plot(scope='dmri_rsi.nd_fiber.at_fmaj')
dmri_rsi.nd_fiber.at_fmaj: 10689 rows
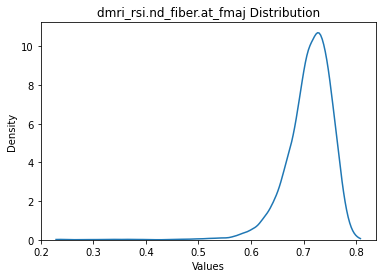
How about we apply just a strict criteria of say 10 std.
[16]:
data.filter_outliers_by_std(scope='data', n_std=10, inplace=True)
Dropped 26 Rows
Define a Test set.#
In this example project we are going to test a bunch of different Machine Learning Pipeline’s. In order to avoid meta-issues of overfitting onto our dataset, we will therefore define a train-test split. The train set we will use to try different pipelines, then only with the best final pipeline will we use the test set.
We will impose one extra constraint when applying the test split, namely that members of the same family, i.e., those with the same family id, stay in the same training or testing fold.
[17]:
# We use this to say we want to preserve families
preserve_family = bp.CVStrategy(groups='rel_family_id')
# Apply the test split
data = data.set_test_split(size=.2,
cv_strategy=preserve_family,
random_state=6)
data
Performing test split on: 10663 subjects.
random_state: 6
Test split size: 0.2
Performed train/test split
Train size: 8562
Test size: 2101
[17]:
Data
| dmri_rsi.n0_fiber.at_allfib.lh | dmri_rsi.n0_fiber.at_allfib.rh | dmri_rsi.n0_fiber.at_allfibers | dmri_rsi.n0_fiber.at_allfibnocc.lh | dmri_rsi.n0_fiber.at_allfibnocc.rh | dmri_rsi.n0_fiber.at_atr.lh | dmri_rsi.n0_fiber.at_atr.rh | dmri_rsi.n0_fiber.at_cc | dmri_rsi.n0_fiber.at_cgc.lh | dmri_rsi.n0_fiber.at_cgc.rh | ... | dmri_rsi.vol_fiber.at_scs.lh | dmri_rsi.vol_fiber.at_scs.rh | dmri_rsi.vol_fiber.at_sifc.lh | dmri_rsi.vol_fiber.at_sifc.rh | dmri_rsi.vol_fiber.at_slf.lh | dmri_rsi.vol_fiber.at_slf.rh | dmri_rsi.vol_fiber.at_tslf.lh | dmri_rsi.vol_fiber.at_tslf.rh | dmri_rsi.vol_fiber.at_unc.lh | dmri_rsi.vol_fiber.at_unc.rh | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.327623 | 0.323420 | 0.325957 | 0.340559 | 0.332364 | 0.347837 | 0.336072 | 0.306803 | 0.311347 | 0.304854 | ... | 23672.0 | 13056.0 | 9648.0 | 9528.0 | 10152.0 | 11504.0 | 8384.0 | 8024.0 | 4968.0 | 7176.0 |
| 2 | 0.325374 | 0.311465 | 0.319027 | 0.341213 | 0.326334 | 0.346651 | 0.335362 | 0.288124 | 0.326416 | 0.300990 | ... | 33112.0 | 19256.0 | 11928.0 | 8688.0 | 13144.0 | 15344.0 | 10488.0 | 10936.0 | 6904.0 | 9480.0 |
| 3 | 0.305095 | 0.304357 | 0.305170 | 0.315477 | 0.312866 | 0.313972 | 0.316729 | 0.288742 | 0.289166 | 0.290347 | ... | 28480.0 | 16016.0 | 13024.0 | 11960.0 | 13600.0 | 14880.0 | 11416.0 | 10592.0 | 6952.0 | 8736.0 |
| 4 | 0.316860 | 0.315238 | 0.316399 | 0.328251 | 0.327259 | 0.333998 | 0.318162 | 0.294008 | 0.297800 | 0.299230 | ... | 29904.0 | 17968.0 | 12720.0 | 11336.0 | 13528.0 | 15672.0 | 11096.0 | 11816.0 | 5912.0 | 7336.0 |
| 5 | 0.323521 | 0.326741 | 0.325466 | 0.336003 | 0.335291 | 0.326243 | 0.337367 | 0.305382 | 0.311843 | 0.315721 | ... | 23048.0 | 12032.0 | 9056.0 | 9248.0 | 9672.0 | 11048.0 | 7848.0 | 7520.0 | 5088.0 | 7448.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 11870 | 0.335741 | 0.336048 | 0.336372 | 0.349806 | 0.347732 | 0.349966 | 0.345692 | 0.312056 | 0.324054 | 0.336676 | ... | 28328.0 | 15400.0 | 9656.0 | 10080.0 | 11312.0 | 13496.0 | 8728.0 | 9176.0 | 4960.0 | 7392.0 |
| 11871 | 0.320563 | 0.317525 | 0.319429 | 0.327302 | 0.322161 | 0.333086 | 0.315482 | 0.308554 | 0.299938 | 0.298093 | ... | 23792.0 | 13632.0 | 9928.0 | 8912.0 | 9152.0 | 12288.0 | 7128.0 | 8912.0 | 5744.0 | 7376.0 |
| 11872 | 0.327051 | 0.325386 | 0.326522 | 0.340918 | 0.334854 | 0.345435 | 0.335610 | 0.305720 | 0.308630 | 0.330612 | ... | 28640.0 | 16384.0 | 9496.0 | 11216.0 | 12168.0 | 12312.0 | 9520.0 | 8952.0 | 4568.0 | 9056.0 |
| 11873 | 0.323579 | 0.319377 | 0.321805 | 0.334945 | 0.329433 | 0.332200 | 0.334017 | 0.304399 | 0.303831 | 0.307037 | ... | 26216.0 | 14672.0 | 9408.0 | 8872.0 | 10960.0 | 12584.0 | 8880.0 | 9176.0 | 3696.0 | 6168.0 |
| 11874 | 0.383537 | 0.371483 | 0.377822 | 0.394413 | 0.373486 | 0.404684 | 0.374435 | 0.366270 | 0.415342 | 0.418280 | ... | 26544.0 | 15624.0 | 9904.0 | 10360.0 | 9904.0 | 12216.0 | 7712.0 | 8000.0 | 5208.0 | 8816.0 |
10663 rows × 294 columns
8562 rows × 294 columns - Train Set
2101 rows × 294 columns - Test Set
Target
| anthro_waist_cm | |
|---|---|
| 0 | 31.00 |
| 2 | 26.75 |
| 3 | 23.50 |
| 4 | 30.00 |
| 5 | 28.00 |
| ... | ... |
| 11870 | 26.00 |
| 11871 | 30.00 |
| 11872 | 19.00 |
| 11873 | 25.00 |
| 11874 | 32.00 |
10663 rows × 1 columns
8562 rows × 1 columns - Train Set
2101 rows × 1 columns - Test Set
Non Input
| rel_family_id | sex | |
|---|---|---|
| 0 | 7321 | 0 |
| 2 | 3971 | 1 |
| 3 | 3139 | 1 |
| 4 | 4543 | 1 |
| 5 | 1933 | 1 |
| ... | ... | ... |
| 11870 | 3128 | 1 |
| 11871 | 2111 | 0 |
| 11872 | 5907 | 0 |
| 11873 | 5594 | 0 |
| 11874 | 6238 | 0 |
10663 rows × 2 columns
8562 rows × 2 columns - Train Set
2101 rows × 2 columns - Test Set
Evaluate Different Pipelines#
First let’s save some commonly used parameters in an object called the ProblemSpec, we will use all defaults except for the number of jobs, for that let’s use n_jobs=8.
[18]:
ps = bp.ProblemSpec(n_jobs=8)
The function we will use to evaluate different pipelines is bp.evaluate, let’s start with an example with just a linear regression model.
[19]:
linear_model = bp.Model('linear')
results = bp.evaluate(pipeline=linear_model,
dataset=data,
problem_spec=ps,
eval_verbose=1)
results
Predicting target = anthro_waist_cm
Using problem_type = regression
Using scope = all defining an initial total of 294 features.
Evaluating 8562 total data points.
Train size = 6849
Val size = 1713
Fit fold in 0.068 seconds.
explained_variance: 0.19228859349221128
neg_mean_squared_error: -14.42743864665399
Train size = 6849
Val size = 1713
Fit fold in 0.081 seconds.
explained_variance: 0.21135734492931657
neg_mean_squared_error: -13.96475127488305
Train size = 6850
Val size = 1712
Fit fold in 0.085 seconds.
explained_variance: 0.19187172345658088
neg_mean_squared_error: -13.996165486455398
Train size = 6850
Val size = 1712
Fit fold in 0.071 seconds.
explained_variance: 0.16100380766529065
neg_mean_squared_error: -13.915570852834366
Train size = 6850
Val size = 1712
Fit fold in 0.099 seconds.
explained_variance: 0.21448693993841805
neg_mean_squared_error: -13.570138682760142
[19]:
BPtEvaluator
------------
mean_scores = {'explained_variance': 0.1942016818963635, 'neg_mean_squared_error': -13.974812988717389}
std_scores = {'explained_variance': 0.019063031946510073, 'neg_mean_squared_error': 0.27301944181081267}
Saved Attributes: ['estimators', 'preds', 'timing', 'train_subjects', 'val_subjects', 'feat_names', 'ps', 'mean_scores', 'std_scores', 'weighted_mean_scores', 'scores', 'fis_', 'coef_']
Available Methods: ['get_preds_dfs', 'get_fis', 'get_coef_', 'permutation_importance']
Evaluated with:
ProblemSpec(n_jobs=8, problem_type='regression',
scorer={'explained_variance': make_scorer(explained_variance_score),
'neg_mean_squared_error': make_scorer(mean_squared_error, greater_is_better=False)},
subjects='train', target='anthro_waist_cm')
Note from the verbose output that it has correctly detected a number of things including: a regression problem type, that we only want to use the training set, that we want to use all input features, what the target variable is, ect…
We get an instance of BPtEvaluator with the results. This stores all kinds of different information, for example:
[20]:
# Beta weights
results.get_fis()
[20]:
| dmri_rsi.n0_fiber.at_allfib.lh | dmri_rsi.n0_fiber.at_allfib.rh | dmri_rsi.n0_fiber.at_allfibers | dmri_rsi.n0_fiber.at_allfibnocc.lh | dmri_rsi.n0_fiber.at_allfibnocc.rh | dmri_rsi.n0_fiber.at_atr.lh | dmri_rsi.n0_fiber.at_atr.rh | dmri_rsi.n0_fiber.at_cc | dmri_rsi.n0_fiber.at_cgc.lh | dmri_rsi.n0_fiber.at_cgc.rh | ... | dmri_rsi.vol_fiber.at_scs.lh | dmri_rsi.vol_fiber.at_scs.rh | dmri_rsi.vol_fiber.at_sifc.lh | dmri_rsi.vol_fiber.at_sifc.rh | dmri_rsi.vol_fiber.at_slf.lh | dmri_rsi.vol_fiber.at_slf.rh | dmri_rsi.vol_fiber.at_tslf.lh | dmri_rsi.vol_fiber.at_tslf.rh | dmri_rsi.vol_fiber.at_unc.lh | dmri_rsi.vol_fiber.at_unc.rh | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 13.658717 | 10.182917 | 11.113703 | 2.741103 | 2.096137 | 0.652331 | -19.689333 | 18.133593 | 6.170156 | 18.584436 | ... | 0.000343 | -0.000589 | 0.000551 | 0.000348 | -0.000216 | 0.000278 | 1.902580e-04 | -0.000544 | 0.000643 | 0.000572 |
| 1 | 13.386769 | -7.807120 | 5.590872 | 2.074826 | 1.611921 | -5.200155 | -17.350840 | 18.954327 | 4.418044 | 18.556810 | ... | 0.000263 | -0.000505 | 0.000523 | 0.000272 | -0.000371 | 0.000474 | 1.721382e-04 | -0.000582 | 0.000530 | 0.000525 |
| 2 | 14.601005 | 6.447403 | 6.566593 | 5.105803 | 2.144557 | -0.249971 | -17.505516 | 19.815592 | 10.121972 | 15.690188 | ... | 0.000319 | -0.000600 | 0.000455 | 0.000446 | -0.000303 | 0.000618 | 1.192093e-07 | -0.000615 | 0.000378 | 0.000662 |
| 3 | 12.660464 | 16.193197 | -0.193520 | 2.184492 | 3.968235 | -7.643031 | -16.103781 | 15.539372 | 9.867133 | 14.523899 | ... | 0.000341 | -0.000441 | 0.000587 | 0.000453 | -0.000284 | 0.000608 | 1.287460e-04 | -0.000701 | 0.000359 | 0.000616 |
| 4 | 16.212349 | 11.518905 | 7.905156 | 6.085897 | 1.294112 | -8.058172 | -11.786942 | 13.227197 | 10.812229 | 12.374775 | ... | 0.000080 | -0.000515 | 0.000614 | 0.000411 | -0.000342 | 0.000784 | 2.737045e-04 | -0.000738 | 0.000555 | 0.000540 |
5 rows × 294 columns
[21]:
# Raw predictions made from each fold
results.get_preds_dfs()[0]
[21]:
| predict | y_true | |
|---|---|---|
| 28 | 24.345831 | 21.25 |
| 33 | 24.806902 | 24.50 |
| 36 | 26.968584 | 23.00 |
| 40 | 27.805948 | 30.80 |
| 47 | 25.691679 | 20.00 |
| ... | ... | ... |
| 11848 | 28.006598 | 25.50 |
| 11851 | 23.925535 | 24.00 |
| 11855 | 30.389437 | 38.80 |
| 11861 | 25.687609 | 26.00 |
| 11868 | 29.838160 | 35.00 |
1713 rows × 2 columns
All options are listed under: ‘Saved Attributes’ and ‘Available Methods’.
Anyways, let’s continue trying different models. We will use a ridge regression model. Let’s also use the fact that the jupyter notebook is defining variables in global scope to clean up the evaluation code a bit so we don’t have to keep copy and pasting it.
[22]:
def eval_pipe(pipeline, **kwargs):
return bp.evaluate(pipeline=pipeline,
dataset=data,
problem_spec=ps,
**kwargs)
[23]:
ridge_model = bp.Model('ridge')
# Add standard scaler before ridge model
# We want this because the same amount of regularization is used across features
ridge_pipe = bp.Pipeline([bp.Scaler('standard'), ridge_model])
eval_pipe(ridge_pipe)
[23]:
BPtEvaluator
------------
mean_scores = {'explained_variance': 0.2290475271430472, 'neg_mean_squared_error': -13.362139348686418}
std_scores = {'explained_variance': 0.02075351765737852, 'neg_mean_squared_error': 0.3531711520267176}
Saved Attributes: ['estimators', 'preds', 'timing', 'train_subjects', 'val_subjects', 'feat_names', 'ps', 'mean_scores', 'std_scores', 'weighted_mean_scores', 'scores', 'fis_', 'coef_']
Available Methods: ['get_preds_dfs', 'get_fis', 'get_coef_', 'permutation_importance']
Evaluated with:
ProblemSpec(n_jobs=8, problem_type='regression',
scorer={'explained_variance': make_scorer(explained_variance_score),
'neg_mean_squared_error': make_scorer(mean_squared_error, greater_is_better=False)},
subjects='train', target='anthro_waist_cm')
The ridge regression has hyper-parameters though, what if just whatever the default value is, is not a good choice? We can add a parameter search to the model object.
[24]:
random_search = bp.ParamSearch('RandomSearch', n_iter=64)
ridge_search_model = bp.Model('ridge',
params=1, # Referring to a preset distribution of hyper-params
param_search=random_search)
ridge_search_pipe = bp.Pipeline([bp.Scaler('standard'), ridge_search_model])
eval_pipe(ridge_search_pipe)
[24]:
BPtEvaluator
------------
mean_scores = {'explained_variance': 0.22819416633537087, 'neg_mean_squared_error': -13.376954871269001}
std_scores = {'explained_variance': 0.020902924658044268, 'neg_mean_squared_error': 0.3519917172539553}
Saved Attributes: ['estimators', 'preds', 'timing', 'train_subjects', 'val_subjects', 'feat_names', 'ps', 'mean_scores', 'std_scores', 'weighted_mean_scores', 'scores', 'fis_', 'coef_']
Available Methods: ['get_preds_dfs', 'get_fis', 'get_coef_', 'permutation_importance']
Evaluated with:
ProblemSpec(n_jobs=8, problem_type='regression',
scorer={'explained_variance': make_scorer(explained_variance_score),
'neg_mean_squared_error': make_scorer(mean_squared_error, greater_is_better=False)},
subjects='train', target='anthro_waist_cm')
At any point we can also ask different questions, for example: What happens we evaluate the model on only one sex?
[25]:
# Male only model first
eval_pipe(ridge_search_pipe,
subjects=bp.ValueSubset('sex', 'M', decode_values=True))
[25]:
BPtEvaluator
------------
mean_scores = {'explained_variance': 0.2213861522565453, 'neg_mean_squared_error': -13.339620278920432}
std_scores = {'explained_variance': 0.038899168304109256, 'neg_mean_squared_error': 0.2880607358773867}
Saved Attributes: ['estimators', 'preds', 'timing', 'train_subjects', 'val_subjects', 'feat_names', 'ps', 'mean_scores', 'std_scores', 'weighted_mean_scores', 'scores', 'fis_', 'coef_']
Available Methods: ['get_preds_dfs', 'get_fis', 'get_coef_', 'permutation_importance']
Evaluated with:
ProblemSpec(n_jobs=8, problem_type='regression',
scorer={'explained_variance': make_scorer(explained_variance_score),
'neg_mean_squared_error': make_scorer(mean_squared_error, greater_is_better=False)},
subjects=ValueSubset(name=sex, values=M, decode_values=True),
target='anthro_waist_cm')
[26]:
eval_pipe(ridge_search_pipe,
subjects=bp.ValueSubset('sex', 'F', decode_values=True))
[26]:
BPtEvaluator
------------
mean_scores = {'explained_variance': 0.23205991889705402, 'neg_mean_squared_error': -13.996539808005668}
std_scores = {'explained_variance': 0.022888054425128167, 'neg_mean_squared_error': 0.5720979643373396}
Saved Attributes: ['estimators', 'preds', 'timing', 'train_subjects', 'val_subjects', 'feat_names', 'ps', 'mean_scores', 'std_scores', 'weighted_mean_scores', 'scores', 'fis_', 'coef_']
Available Methods: ['get_preds_dfs', 'get_fis', 'get_coef_', 'permutation_importance']
Evaluated with:
ProblemSpec(n_jobs=8, problem_type='regression',
scorer={'explained_variance': make_scorer(explained_variance_score),
'neg_mean_squared_error': make_scorer(mean_squared_error, greater_is_better=False)},
subjects=ValueSubset(name=sex, values=F, decode_values=True),
target='anthro_waist_cm')
We do see a decrease in performance for the male model, though it is a bit difficult to tell if that is just noise, or related to the smaller sample sizes. Atleast the results are close, which tells us that sex likely is not being exploited as a proxy! For example if we ran the two same sex only models and they did terrible, it would tell us that our original model had been just memorizing sex effects.
Let’s try a different choice of scaler next.
[27]:
ridge_search_pipe = bp.Pipeline([bp.Scaler('robust'), ridge_search_model])
eval_pipe(ridge_search_pipe)
[27]:
BPtEvaluator
------------
mean_scores = {'explained_variance': 0.22756821907365027, 'neg_mean_squared_error': -13.388315785245691}
std_scores = {'explained_variance': 0.02147974464145115, 'neg_mean_squared_error': 0.36072359437215784}
Saved Attributes: ['estimators', 'preds', 'timing', 'train_subjects', 'val_subjects', 'feat_names', 'ps', 'mean_scores', 'std_scores', 'weighted_mean_scores', 'scores', 'fis_', 'coef_']
Available Methods: ['get_preds_dfs', 'get_fis', 'get_coef_', 'permutation_importance']
Evaluated with:
ProblemSpec(n_jobs=8, problem_type='regression',
scorer={'explained_variance': make_scorer(explained_variance_score),
'neg_mean_squared_error': make_scorer(mean_squared_error, greater_is_better=False)},
subjects='train', target='anthro_waist_cm')
[28]:
ridge_search_pipe = bp.Pipeline([bp.Scaler('quantile norm'), ridge_search_model])
eval_pipe(ridge_search_pipe)
[28]:
BPtEvaluator
------------
mean_scores = {'explained_variance': 0.24424142049591255, 'neg_mean_squared_error': -13.10554322507986}
std_scores = {'explained_variance': 0.014347568570678794, 'neg_mean_squared_error': 0.33520468336717396}
Saved Attributes: ['estimators', 'preds', 'timing', 'train_subjects', 'val_subjects', 'feat_names', 'ps', 'mean_scores', 'std_scores', 'weighted_mean_scores', 'scores', 'fis_', 'coef_']
Available Methods: ['get_preds_dfs', 'get_fis', 'get_coef_', 'permutation_importance']
Evaluated with:
ProblemSpec(n_jobs=8, problem_type='regression',
scorer={'explained_variance': make_scorer(explained_variance_score),
'neg_mean_squared_error': make_scorer(mean_squared_error, greater_is_better=False)},
subjects='train', target='anthro_waist_cm')
Okay so far we arn’t really seeing sweeping differences when any of the parameters are changed, what about if we try some different complete models as well? Let’s also start off by using some full default pipelines. We can see options with:
[29]:
from BPt.default.pipelines import pipelines
list(pipelines)
[29]:
['elastic_pipe',
'ridge_pipe',
'lgbm_pipe',
'svm_pipe',
'stacking_pipe',
'compare_pipe']
Let’s try the elastic net first.
[30]:
from BPt.default.pipelines import elastic_pipe
elastic_pipe
[30]:
Pipeline(steps=[Imputer(obj='mean', scope='float'),
Imputer(obj='median', scope='category'), Scaler(obj='robust'),
Transformer(obj='one hot encoder', scope='category'),
Model(obj='elastic',
param_search=ParamSearch(cv=CV(cv_strategy=CVStrategy()),
n_iter=60),
params=1)])
We can see that this object has imputation and also a one hot enocer for categorical variables built in. In our case those will just be skipped.
[31]:
eval_pipe(elastic_pipe)
[31]:
BPtEvaluator
------------
mean_scores = {'explained_variance': 0.2149350643892411, 'neg_mean_squared_error': -13.612086079062005}
std_scores = {'explained_variance': 0.017456542194885176, 'neg_mean_squared_error': 0.30452126404963037}
Saved Attributes: ['estimators', 'preds', 'timing', 'train_subjects', 'val_subjects', 'feat_names', 'ps', 'mean_scores', 'std_scores', 'weighted_mean_scores', 'scores', 'fis_', 'coef_']
Available Methods: ['get_preds_dfs', 'get_fis', 'get_coef_', 'permutation_importance']
Evaluated with:
ProblemSpec(n_jobs=8, problem_type='regression',
scorer={'explained_variance': make_scorer(explained_variance_score),
'neg_mean_squared_error': make_scorer(mean_squared_error, greater_is_better=False)},
subjects='train', target='anthro_waist_cm')
Let’s try a light gbm model next
[32]:
from BPt.default.pipelines import lgbm_pipe
eval_pipe(lgbm_pipe)
[32]:
BPtEvaluator
------------
mean_scores = {'explained_variance': 0.15981886810855045, 'neg_mean_squared_error': -14.628174890288136}
std_scores = {'explained_variance': 0.008612472597788492, 'neg_mean_squared_error': 0.3176639245894241}
Saved Attributes: ['estimators', 'preds', 'timing', 'train_subjects', 'val_subjects', 'feat_names', 'ps', 'mean_scores', 'std_scores', 'weighted_mean_scores', 'scores', 'fis_', 'feature_importances_']
Available Methods: ['get_preds_dfs', 'get_fis', 'get_feature_importances', 'permutation_importance']
Evaluated with:
ProblemSpec(n_jobs=8, problem_type='regression',
scorer={'explained_variance': make_scorer(explained_variance_score),
'neg_mean_squared_error': make_scorer(mean_squared_error, greater_is_better=False)},
subjects='train', target='anthro_waist_cm')
non-linear svm?
[33]:
from BPt.default.pipelines import svm_pipe
eval_pipe(svm_pipe)
[33]:
BPtEvaluator
------------
mean_scores = {'explained_variance': 0.23972557599885516, 'neg_mean_squared_error': -13.404542506122965}
std_scores = {'explained_variance': 0.025086520458320005, 'neg_mean_squared_error': 0.41542931615444495}
Saved Attributes: ['estimators', 'preds', 'timing', 'train_subjects', 'val_subjects', 'feat_names', 'ps', 'mean_scores', 'std_scores', 'weighted_mean_scores', 'scores']
Available Methods: ['get_preds_dfs', 'permutation_importance']
Evaluated with:
ProblemSpec(n_jobs=8, problem_type='regression',
scorer={'explained_variance': make_scorer(explained_variance_score),
'neg_mean_squared_error': make_scorer(mean_squared_error, greater_is_better=False)},
subjects='train', target='anthro_waist_cm')
How about a linear svm?
[34]:
sgd_pipe = bp.Pipeline([bp.Scaler('robust'),
bp.Model('linear svm', params=1, param_search=random_search)])
eval_pipe(sgd_pipe)
[34]:
BPtEvaluator
------------
mean_scores = {'explained_variance': 0.22686726044873592, 'neg_mean_squared_error': -13.632092635620277}
std_scores = {'explained_variance': 0.015546983038273305, 'neg_mean_squared_error': 0.28724921946194054}
Saved Attributes: ['estimators', 'preds', 'timing', 'train_subjects', 'val_subjects', 'feat_names', 'ps', 'mean_scores', 'std_scores', 'weighted_mean_scores', 'scores', 'fis_', 'coef_']
Available Methods: ['get_preds_dfs', 'get_fis', 'get_coef_', 'permutation_importance']
Evaluated with:
ProblemSpec(n_jobs=8, problem_type='regression',
scorer={'explained_variance': make_scorer(explained_variance_score),
'neg_mean_squared_error': make_scorer(mean_squared_error, greater_is_better=False)},
subjects='train', target='anthro_waist_cm')
Compare#
We can also notably achieve a lot of the different modelling steps we just took, but in a much cleaner way, that is through special Compare input objects. For example let’s run the comparisons between a few models. Compare basically does a grid search over all of the parameters, but in contrast to setting up the different options as a nested grid search, the full 5-fold CV is run for every combination.
[35]:
# Define a set of bp.Options as wrapped in bp.Compare
compare_pipes = bp.Compare([bp.Option(sgd_pipe, name='sgd'),
bp.Option(ridge_search_pipe, name='ridge'),
bp.Option(elastic_pipe, name='elastic'),
bp.Option(lgbm_pipe, name='lgbm')])
# Pass as before as if a pipeline
results = eval_pipe(compare_pipes)
results.summary()
[35]:
| mean_scores_explained_variance | mean_scores_neg_mean_squared_error | std_scores_explained_variance | std_scores_neg_mean_squared_error | mean_timing_fit | mean_timing_score | |
|---|---|---|---|---|---|---|
| pipeline | ||||||
| sgd | 0.226867 | -13.632093 | 0.015547 | 0.287249 | 16.182405 | 0.007756 |
| ridge | 0.244241 | -13.105543 | 0.014348 | 0.335205 | 11.024628 | 0.461483 |
| elastic | 0.214935 | -13.612086 | 0.017457 | 0.304521 | 8.584299 | 0.036844 |
| lgbm | 0.159819 | -14.628175 | 0.008612 | 0.317664 | 30.417882 | 0.063121 |
Applying the Test Set#
So far we have been only running internal 5-fold CV on the training set. What if we say we are done with exploration, and now we want to essentially confirm that our best model we have found through internal CV on the training set generalizes to a set of unseen data. To do this, we re-train the best model tested on the full training set and test it on the testing set. In BPt this is done by just passing cv=‘test’ to evaluate.
[36]:
results = eval_pipe(ridge_search_pipe, cv='test', eval_verbose=1)
results
Predicting target = anthro_waist_cm
Using problem_type = regression
Using scope = all defining an initial total of 294 features.
Evaluating 10663 total data points.
Train size = 8562
Val size = 2101
Fit fold in 13.486 seconds.
explained_variance: 0.269340472039553
neg_mean_squared_error: -13.932075034752192
[36]:
BPtEvaluator
------------
mean_scores = {'explained_variance': 0.269340472039553, 'neg_mean_squared_error': -13.932075034752192}
std_scores = {'explained_variance': 0.0, 'neg_mean_squared_error': 0.0}
Saved Attributes: ['estimators', 'preds', 'timing', 'train_subjects', 'val_subjects', 'feat_names', 'ps', 'mean_scores', 'std_scores', 'weighted_mean_scores', 'scores', 'fis_', 'coef_']
Available Methods: ['get_preds_dfs', 'get_fis', 'get_coef_', 'permutation_importance']
Evaluated with:
ProblemSpec(n_jobs=8, problem_type='regression',
scorer={'explained_variance': make_scorer(explained_variance_score),
'neg_mean_squared_error': make_scorer(mean_squared_error, greater_is_better=False)},
subjects='all', target='anthro_waist_cm')