Results by Pipeline

We break down the base results here by pipeline (instead of parcellation type) in two different ways: Intra and Inter pipeline (corresponding to the top and bottom of the figure below). If necessary first see the intro to results page for a guide on how the results in this project are interpreted.

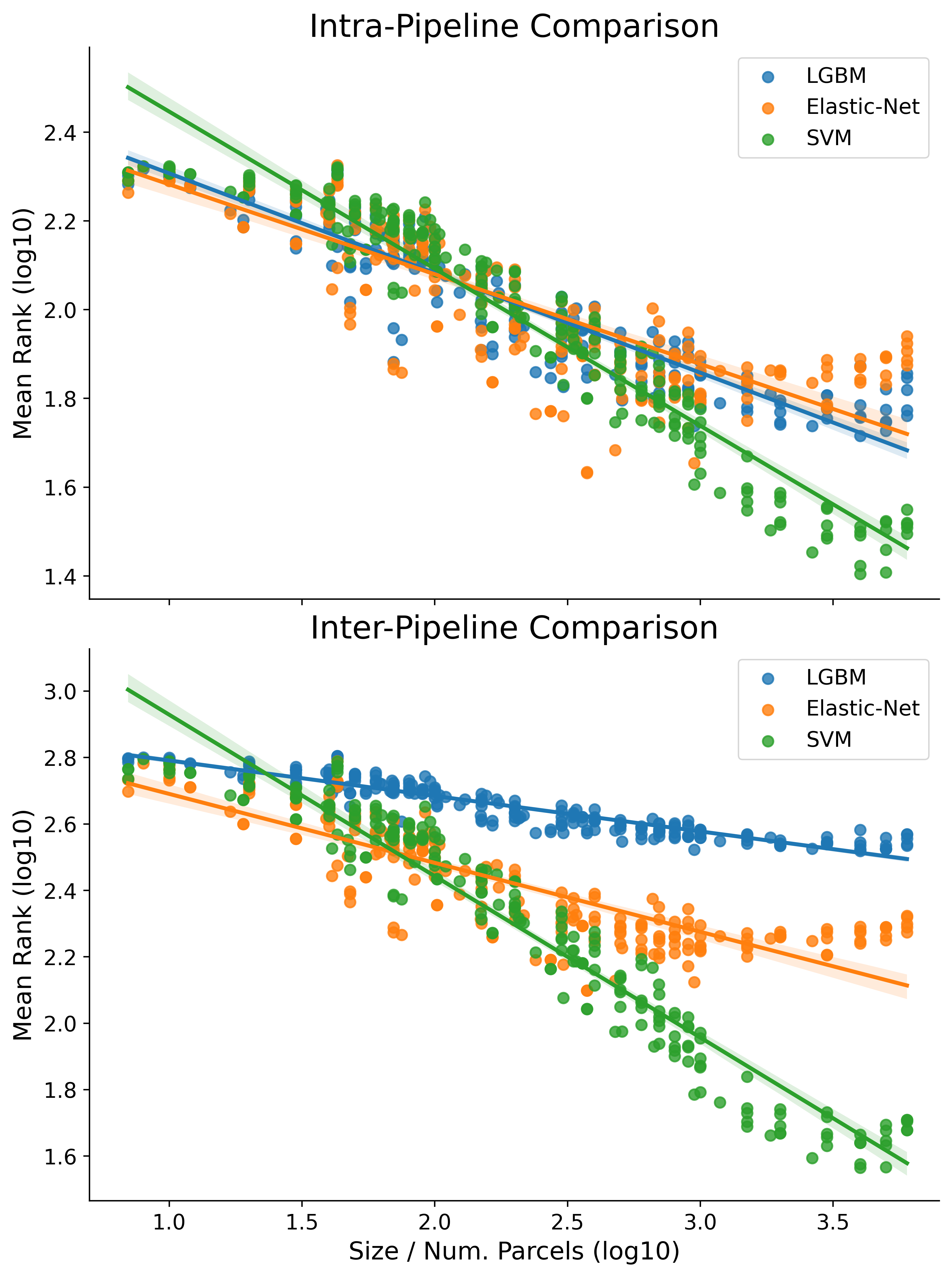
By Pipeline

Intra-Pipeline Comparison

When comparing in an intra-pipeline fashion, we are essentially computing the ranks independently for each choice of ML Pipeline. We also estimate the powerlaw region separately for each.

We can then model these results as log10(Mean_Rank) ~ log10(Size) * C(Pipeline) where Pipeline (the type of ML pipeline) is a fixed effect and can interact with Size (Fullscreen Plot Link).

OLS Regression Results
Dep. Variable: Mean_Rank R-squared: 0.882
Model: OLS Adj. R-squared: 0.881
Method: Least Squares F-statistic: 878.8
Date: Mon, 03 Jan 2022 Prob (F-statistic): 2.48e-270

coef std err t P>|t| [0.025 0.975]
Intercept 2.5893 0.019 135.246 0.000 2.552 2.627
C(Pipeline)[T.LGBM] -0.0208 0.026 -0.795 0.427 -0.072 0.031
C(Pipeline)[T.SVM] 0.3020 0.028 10.939 0.000 0.248 0.356
Size -0.2606 0.009 -30.318 0.000 -0.278 -0.244
Size:C(Pipeline)[T.LGBM] 0.0162 0.012 1.405 0.160 -0.006 0.039
Size:C(Pipeline)[T.SVM] -0.1291 0.012 -10.957 0.000 -0.152 -0.106

The resulting statistical table is a little bit difficult to make sense of at first, so let’s also plot the fit to the data to get a better feel.

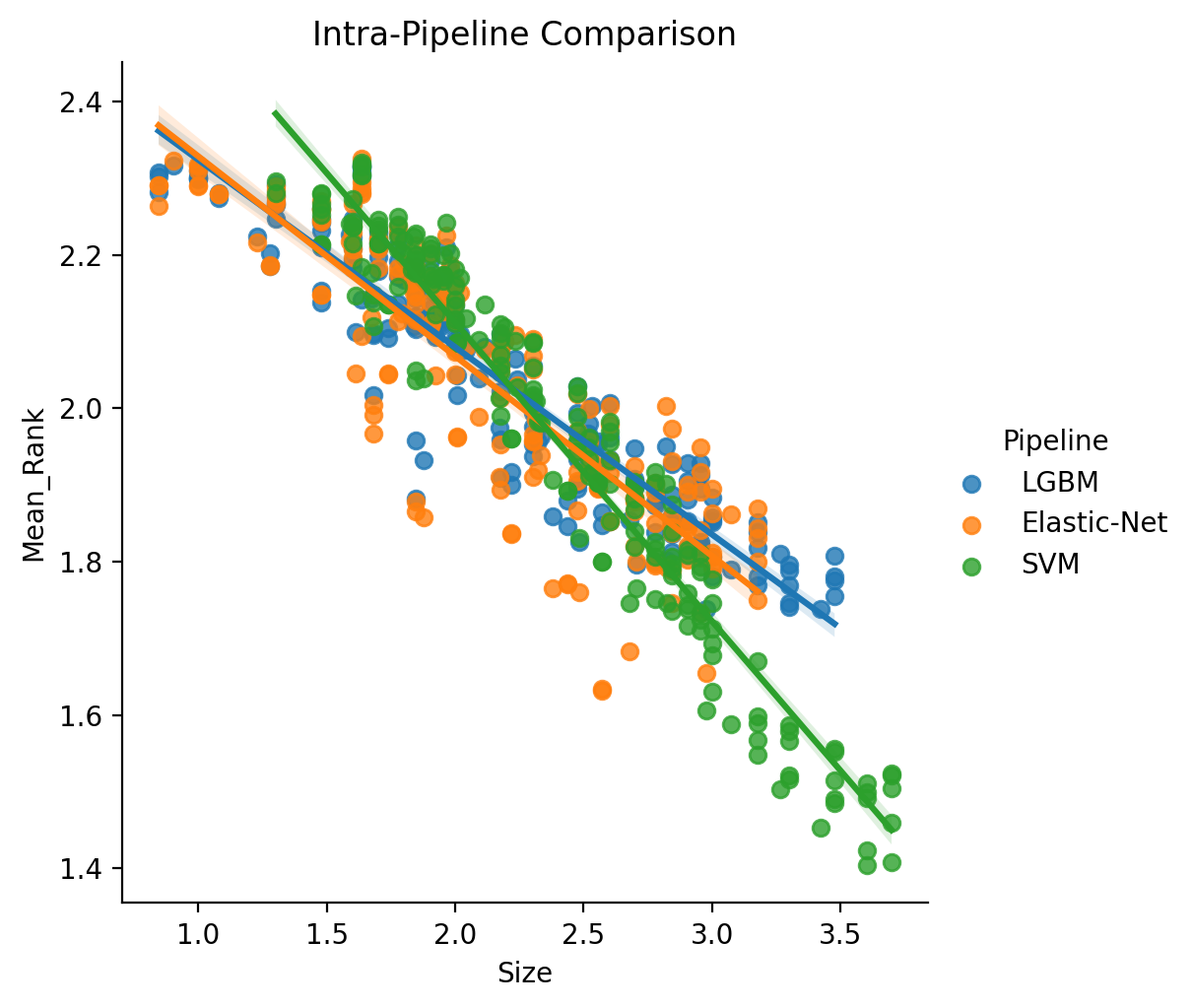
By Pipeline

These results indicate that there are differences between the pipelines (i.e., scaling coefficient, range of scaling and intercept), as well as confirm more generally that scaling, albeit with varying degree, holds regardless of pipeline.

Another interesting way to view how results change when computed separately between pipelines is through an interactive visualization. Click Here for a fullscreen version of the plot.

A nice feature of the interactive plot is that by selecting different pipelines from the toggle, you can watch an animation of how specific results change with with different pipelines. You can also hover over specific data points to find out more information, for example what parcellation that data point corresponds to. You can also find a version of the interactive plot with non log10 axis here.

Inter-Pipeline Comparison

Alternately, we can compute rankings in an inter-pipeline manner, which means that the initial calculating of Rank is determined by directly comparing all Pipeline-Parcellation pairs for each target variable. The key difference here being inter-pipeline’s measure of mean rank as computed over 660 possible ranks versus intra as over 220 possible ranks.

We model these results in the same way as with the intra-pipeline comparison, but importantly using the different computation of mean rank. We also in this case do not estimate a powerlaw region of scaling as here we are more interested in the full statistical comparison. Formula: log10(Mean_Rank) ~ log10(Size) * C(Pipeline).

OLS Regression Results
Dep. Variable: Mean_Rank R-squared: 0.921
Model: OLS Adj. R-squared: 0.921
Method: Least Squares F-statistic: 1527.
Date: Mon, 03 Jan 2022 Prob (F-statistic): 0.00

coef std err t P>|t| [0.025 0.975]
Intercept 2.8836 0.018 160.158 0.000 2.848 2.919
C(Pipeline)[T.LGBM] 0.0107 0.025 0.422 0.673 -0.039 0.061
C(Pipeline)[T.SVM] 0.5203 0.025 20.432 0.000 0.470 0.570
Size -0.2026 0.007 -27.342 0.000 -0.217 -0.188
Size:C(Pipeline)[T.LGBM] 0.0971 0.010 9.267 0.000 0.077 0.118
Size:C(Pipeline)[T.SVM] -0.2798 0.010 -26.707 0.000 -0.300 -0.259

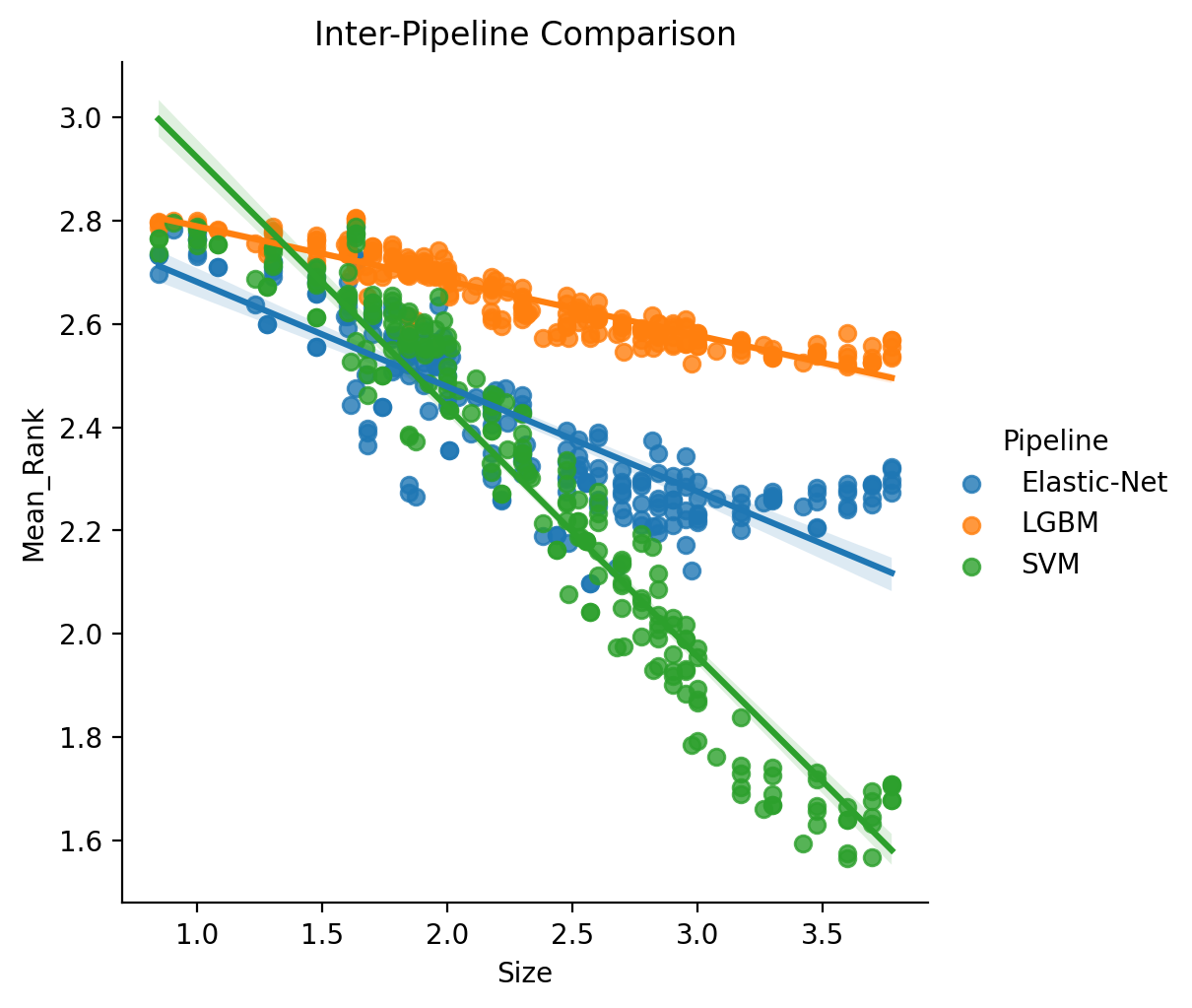
By Pipeline

Extra